Problemas de edades
En este texto vamos a resolver 3 problemas típicos de calcular edades. Los dos primeros problemas se resuelven con una ecuación de primer grado y el tercero mediante un sistema de 2 ecuaciones con 2 incógnitas.
Problema 1
Si dentro de 10 años Adriana tiene el triple de la edad que tiene ahora, ¿qué edad tendrá entonces?
Solución:
Llamamos x a la edad actual de Adriana. Como Adriana tiene ahora x años, dentro de 10 años su edad será x + 10. El triple de la edad que tiene ahora es 3⋅x.
Por tanto, la ecuación que expresa que dentro de 10 años la edad será el triple que la actual es
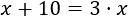 Resolvemos la ecuación:
Resolvemos la ecuación:
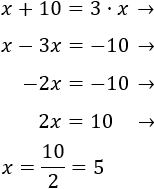 Luego la edad actual de Adriana es 5. Dentro de 10 años, su edad será 15.
Problema 2
La abuela de Lucía tiene 5 veces su edad y su madre tiene la mitad de edad que su abuela. Dentro de 6 años, la edad de la Lucía es la mitad que la de su madre, ¿qué edad tiene cada una?
Solución:
Si la edad de Lucía es x, la de su abuela es 5x y la de su madre es 5x/2. La ecuación que tenemos es
Luego la edad actual de Adriana es 5. Dentro de 10 años, su edad será 15.
Problema 2
La abuela de Lucía tiene 5 veces su edad y su madre tiene la mitad de edad que su abuela. Dentro de 6 años, la edad de la Lucía es la mitad que la de su madre, ¿qué edad tiene cada una?
Solución:
Si la edad de Lucía es x, la de su abuela es 5x y la de su madre es 5x/2. La ecuación que tenemos es
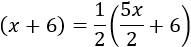 La multiplicamos por 4 para evitar los denominadores:
La multiplicamos por 4 para evitar los denominadores:
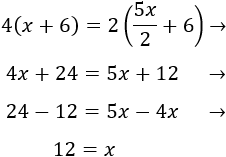 Lucía tiene 12 años, su madre tiene 30 años y su abuela tiene 60.
Problema 3
La suma de las edades de dos hermanos es 28 y la resta de sus edades es 2. ¿Qué edades tienen los hermanos?
Solución:
Si x e y son las edades actuales de los hermanos, su suma es
Lucía tiene 12 años, su madre tiene 30 años y su abuela tiene 60.
Problema 3
La suma de las edades de dos hermanos es 28 y la resta de sus edades es 2. ¿Qué edades tienen los hermanos?
Solución:
Si x e y son las edades actuales de los hermanos, su suma es
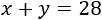 Y la resta de sus edades es
Y la resta de sus edades es
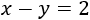 Luego el sistema de ecuaciones del problema es
Luego el sistema de ecuaciones del problema es
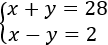 Lo resolvemos por reducción sumando las ecuaciones:
Lo resolvemos por reducción sumando las ecuaciones:
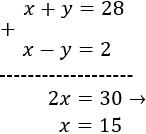 Calculamos la otra incógnita:
Calculamos la otra incógnita:
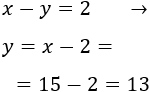 Las edades de los hermanos son 13 y 15.
Enlaces:
Las edades de los hermanos son 13 y 15.
Enlaces:
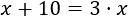 Resolvemos la ecuación:
Resolvemos la ecuación:
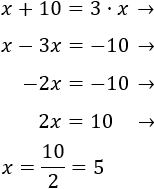 Luego la edad actual de Adriana es 5. Dentro de 10 años, su edad será 15.
Problema 2
La abuela de Lucía tiene 5 veces su edad y su madre tiene la mitad de edad que su abuela. Dentro de 6 años, la edad de la Lucía es la mitad que la de su madre, ¿qué edad tiene cada una?
Solución:
Si la edad de Lucía es x, la de su abuela es 5x y la de su madre es 5x/2. La ecuación que tenemos es
Luego la edad actual de Adriana es 5. Dentro de 10 años, su edad será 15.
Problema 2
La abuela de Lucía tiene 5 veces su edad y su madre tiene la mitad de edad que su abuela. Dentro de 6 años, la edad de la Lucía es la mitad que la de su madre, ¿qué edad tiene cada una?
Solución:
Si la edad de Lucía es x, la de su abuela es 5x y la de su madre es 5x/2. La ecuación que tenemos es
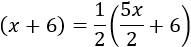 La multiplicamos por 4 para evitar los denominadores:
La multiplicamos por 4 para evitar los denominadores:
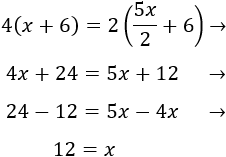 Lucía tiene 12 años, su madre tiene 30 años y su abuela tiene 60.
Problema 3
La suma de las edades de dos hermanos es 28 y la resta de sus edades es 2. ¿Qué edades tienen los hermanos?
Solución:
Si x e y son las edades actuales de los hermanos, su suma es
Lucía tiene 12 años, su madre tiene 30 años y su abuela tiene 60.
Problema 3
La suma de las edades de dos hermanos es 28 y la resta de sus edades es 2. ¿Qué edades tienen los hermanos?
Solución:
Si x e y son las edades actuales de los hermanos, su suma es
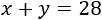 Y la resta de sus edades es
Y la resta de sus edades es
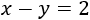 Luego el sistema de ecuaciones del problema es
Luego el sistema de ecuaciones del problema es
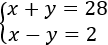 Lo resolvemos por reducción sumando las ecuaciones:
Lo resolvemos por reducción sumando las ecuaciones:
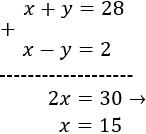 Calculamos la otra incógnita:
Calculamos la otra incógnita:
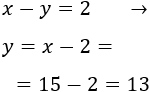 Las edades de los hermanos son 13 y 15.
Enlaces:
Las edades de los hermanos son 13 y 15.
Enlaces:
- Problemas de edades
- 45 problemas de ecuaciones
- Más problemas de ecuaciones
- Problemas de sistemas
- Resolución de ecuaciones
- Resolución de sistemas 2x2
- Problemas y Ecuaciones
- Ecuaciones Resueltas
- Calculadora de porcentajes
- Teorema de Pitágoras online