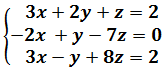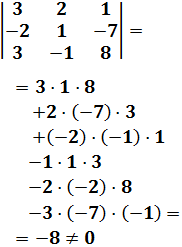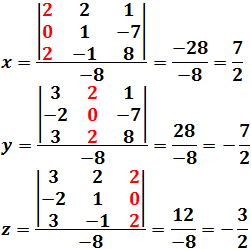Regla de Cramer
1. Introducción
Consideremos el sistema de ecuaciones lineales de dimensión cuadrada, , es decir, el con el mismo número de ecuaciones que de incógnitas. Sabemos que el sistema tiene una única solución (es decir, es compatible determinado) si su matriz de coeficientes, , es regular (su determinante es distinto de 0). En este caso, podemos calcular la solución del sistema mediante la regla de Cramer.
2. La Regla de Cramer
Bajo las condiciones anteriores, consideraremos que las incógnitas son siendo el número de incógnitas del sistema que hemos supuesto que coincide con el número de ecuaciones. Llamamos a la matriz que resulta si a la matriz le cambiamos la columna número por la columna de términos independientes, . Entonces, la regla de Cramer nos proporciona la solución del sistema mediante la fórmula
3. Ejemplo
Consideremos el sistema
El determinante de la matriz de coeficientes es
como es distinto de cero, la matriz es regular y, por tanto, el sistema es compatible determinado.
Calculamos la solución mediante la regla de Cramer:
