Le caratteristiche goniometriche degli angoli
In questo capitolo riprenderemo e consolideremo una prima definizione formale delle grandezze goniometriche.
Un angolo viene normalmente misurato come frazione dell'angolo giro, definito pari a 360°: l'angolo retto è di 90° perché è un quarto di quello di 360°, quello piatto è 180° perché ne è la metà e così via.
Abbiamo visto nei primi esempi che è possibile definire delle altre grandezze che caratterizzano ogni angolo, e che sono molto utili per misurarlo e fare operazioni con esso. Tali grandezze sono dette goniometriche, appunto perché misurano le caratteristiche degli angoli (la radice "gonio" deriva dal greco e significa appunto "angolo", infatti il goniometro è lo strumento per misurare gli angoli). Nella seguente animazione introduciamo la prima di queste grandezze, chiamata "seno" dell'angolo.
Nella seguente animazione riprendiamo le definizioni già anticipate e chiariamo perché possono essere considerate a tutti gli effetti delle caratteristiche specifiche di ogni singolo angolo.
ATTENZIONE: nella seguente animazione verrà costruito un angolo utilizzando segmenti con misure particolari. OVVIAMENTE SI TRATTA DI VALORI DI ESEMPIO, particolarmente utili perché rendono semplici i calcoli, E LE PROPRIETÀ CHE OTTERREMO VALGONO PER QUALSIASI ALTRO ANGOLO.
In questa presentazione abbiamo visto che possiamo definire le caratteristiche di un angolo costruendo sui suoi lati un triangolo rettangolo qualsiasi: da un punto qualsiasi di uno dei suoi due lati tracciamo un segmento perpendicolare all'altro lato. Scegliendo dei punti di partenza differenti otteniamo sempre triangoli simili tra loro, che danno lo stesso valore per ognuna di queste caratteristiche.
In particolare abbiamo definito seno dell'angolo il rapporto tra il cateto opposto all'angolo e l'ipotenusa.
Il seno è quindi collegato al cateto opposto (alla componente "verticale" dell'angolo), e lo si può esprimere anche affermando cheil cateto opposto si ottiene moltiplicando l'ipotenusa per il seno dell'angolo.
Allo stesso modo il rapporto tra il cateto adiacente all'angolo e l'ipotenusa è chiamato coseno dell'angolo.
che si può esprimere anche affermando che il cateto adiacente si ottiene moltiplicando l'ipotenusa per il coseno dell'angolo.
Riportiamo qui l'immagine usata nel capitolo precedente per una prima definizione operativa delle grandezze goniometriche: vediamo ancora una volta che le figure ed i concetti sono gli stessi.
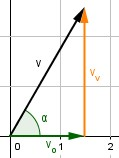
Abbiamo definito , che nel nostro esempio equivaleva a , da cui otteniamo , cioè che la componente verticale (il cateto opposto all'angolo) si ottiene moltiplicando il vettore originale (cioè l'ipotenusa) per un coefficiente che dipende dall'angolo, che abbiamo definito seno dell'angolo .
Allo stesso modo la relazione diventa nel nostro esempio , da cui otteniamo , cioè che la componente orizzontale (il cateto adiacente all'angolo) si ottiene moltiplicando il vettore originale (cioè l'ipotenusa) per un altro coefficiente, che abbiamo definito coseno dell'angolo .
Si definisce infine un'ultima grandezza goniometrica chiamata tangente dell'angolo pari al rapporto tra il cateto opposto e quello adiacente.
Ne approfittiamo per completare la nostra conoscenza dell'angolo di , il primo che abbiamo incontrato. Dato che sappiamo che e , abbiamo che in un triangolo rettangolo con un angolo di si ha che
da cui possiamo calcolare:
Possiamo già intuire che in qualsiasi angolo la tangente può essere calcolata in questo modo, e poiché le due ipotenuse si semplificano sempre, otterremo una di quelle che vengono chiamate leggi fondamentali della goniometria:
VISUALIZZARE LE CARATTERISTICHE DI UN ANGOLO
Utilizzeremo seno, coseno e tangente per risolvere problemi geometrici pratici; è quindi molto importante abituarsi a questi concetti, che propongono un punto di vista un po' differente da quello a cui siamo abituati, e saperli riconoscere ed applicare anche in figure poste in modo "scomodo" (le situazioni reali non sono sempre orientate e su misura rispetto a come siamo comodi noi!).
È quindi importante capire come costruire e visualizzare, dato un angolo qualsiasi, una costruzione che permetta di definire le grandezze goniometriche di quell'angolo.
Facciamo qualche esempio nella seguente animazione.
Puoi allenarti a riconoscere cateto opposto, adiacente ed ipotenusa ed a utilizzarli per calcolare seno, coseno e tangente utilizzando questo strumento:
http://davidpetro.org/WebSketches/TrigGenerator/index.html
LE GRANDEZZE GONIOMETRICHE DI ANGOLI COMPLEMENTARI
Abbiamo visto che seno e coseno siano legati ai cateti di un triangolo rettangolo. Poiché in un qualsiasi triangolo rettangolo i due angoli acuti sono complementari (cioè sommati danno 90°), possiamo dedurne che possiamo usare lo stesso triangolo per studiare le caratteristiche di due angoli complementari, le cui caratteristiche goniometriche sono quindi in relazione tra loro.
L'animazione qui sotto, infatti, mostra che i due angoli acuti dello stesso triangolo rettangolo "si scambiano" il cateto opposto e quello adiacente; di conseguenza il seno di un angolo è il coseno del suo complementare e viceversa.
Nell'animazione è stato introdotto il concetto di cotangente di un angolo, che è definita come il reciproco della tangente.
In modo analogo si definiscono la cosecante come reciproco del seno
e la secante come reciproco del coseno
Queste tre grandezze NON sono così importanti e non le utilizzeremo molto: seno, coseno e tangente sono più che sufficienti per descrivere le caratteristiche degli angoli. È utile conoscerle in modo da poterle interpretare correttamente nel caso le si incontri in un problema o un esercizio.
Molto più importante il concetto generale che abbiamo introdotto studiando gli angoli complementari, ovvero che le caratteristiche di certe coppie di angoli sono in relazione tra loro e si possono ottenere le une dalle altre. Questo è utile per due ragioni:
Ci permette di conoscere i valori goniometrici di nuovi angoli. Ad esempio sapevamo già che , e ; ora da queste possiamo dedurre le caratteristiche del complementare di , cioè , e cioè: