Explorer la translation
Le but de cette leçon est d'explorer la translation. À chaque étape, assure-toi de bien compendre avant de poursuivre. N'hésite pas à retourner en arrière pour revoir une notion ou manipuler davantage. À la fin de cette leçon, tu devras faire des translation avec tes instruments de géométriques. Observe donc attentivement afin de découvrir comment fonctionne la translation.
Définition
La translation est une transformation géométrique qui permet d'obtenir une figure image à partir du «glissement» de la figure initiale.
La translation peut être défini par une flèche de translation qui indique:
- la direction du déplacement par son inclinaison;
- le sens du déplacement par sa pointe;
- la distance entre les points homologues de la figure initiale et de la figure image par sa longueur.
Après avoir suffisament manipuler, réponds aux questions suivantes dans ton cahier d'exercices.
- Que remarques-tu au sujet du segment qui relie un point de la figure initiale à son point homologue dans la figure image, par exemple le segment AA'? Il y a au moins deux choses que tu devrais remarquer.
- Compare les côtés homologues. Que remarques-tu?
- Compare l'ordre des sommets dans la figure initiale et la figure image. Que remarques-tu?
- Quel effet a la position de la flèche de translation dans le plan?
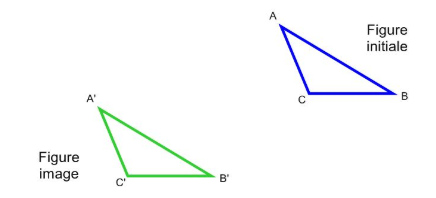
Comment pourrais-tu retrouver la flèche de translation qui a été utilisée lors de la construction ci-dessous?
Translations équivalentes
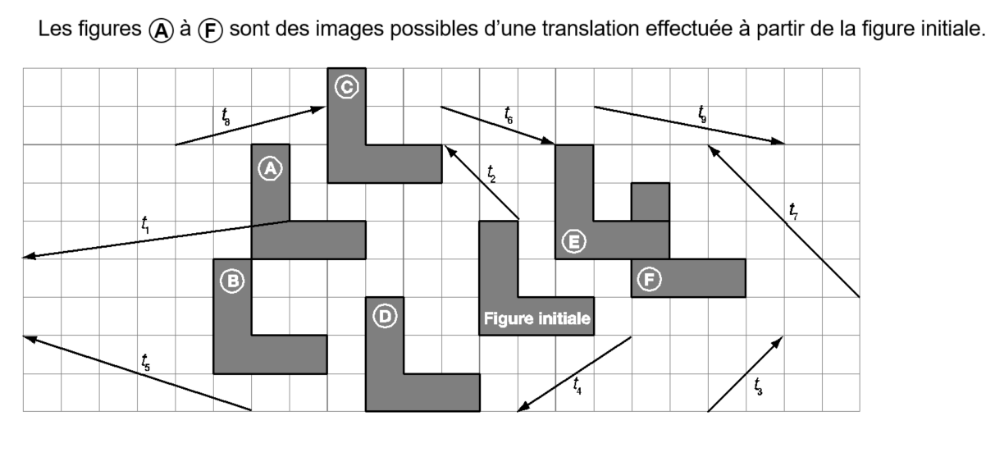
Deux translations sont dites équivalentes si elles ont le même effet sur la figure initiale. Dans ce cas, on dira aussi que les vecteurs de translation sont équivalents.
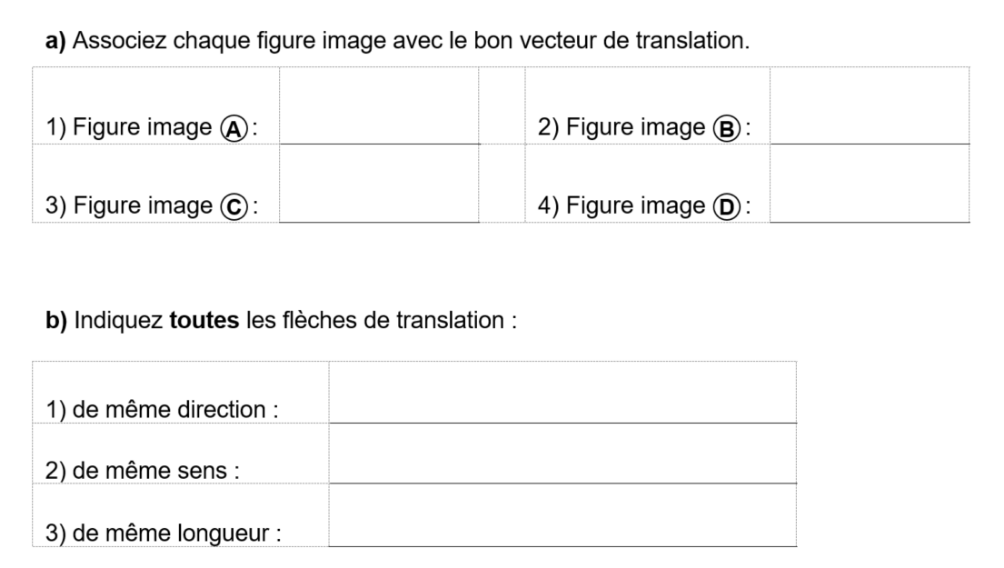
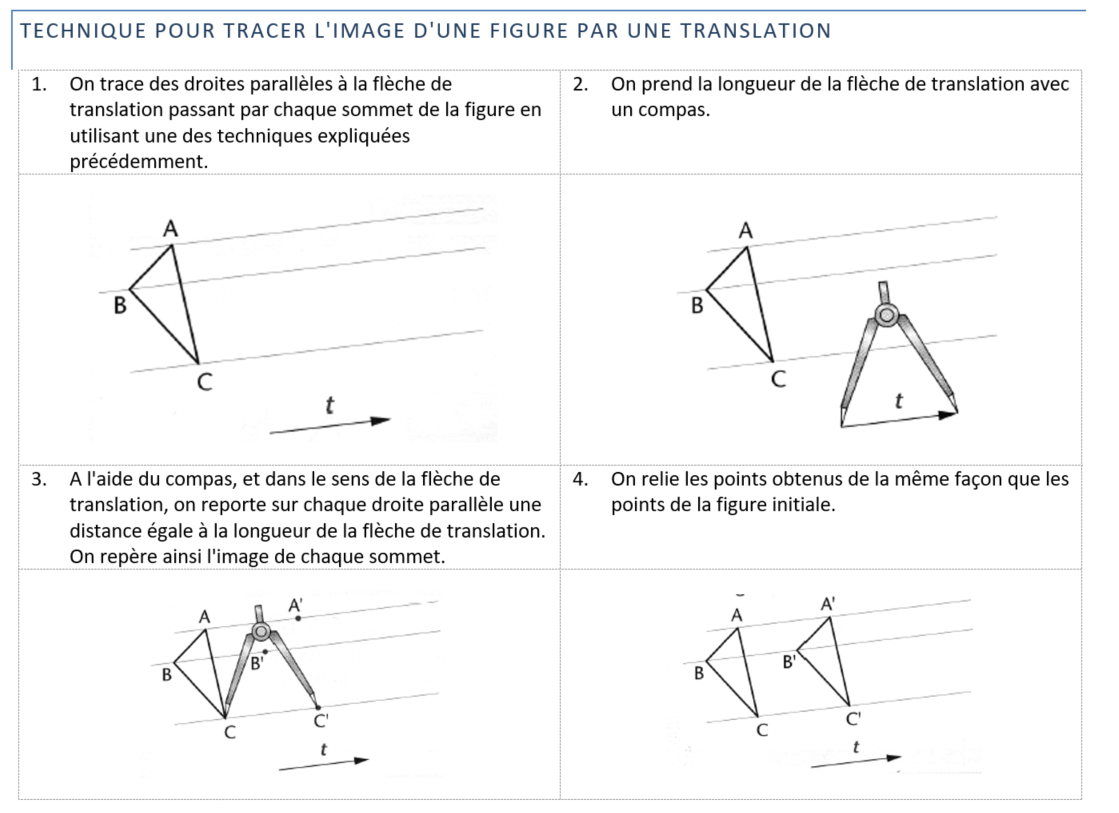
Voici maintenant comment faire une translation avec les instruments de géométrie. La technique est dans tes notes de cours p. 60. Il y a également une bonne vidéo sur le site d'AlloProf.
Tu dois maintenant faire le numéro 3 du devoir 'Les transformations géométriques'.
Devoir:
Faire page 1 du document 'Les transformations géométriques avec les instruments de géométrie'