Outline
GAME THEORY TABLES
GAME THEORY BI-MATRICES
This book is a collection of applets on Game Theory normal form representations.
Only games with two players have been considered.
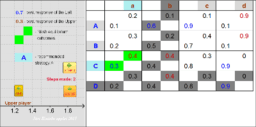
The first applet considers up to 4x4 bi-matrices (games with up to 4 strategies for both players).
To solve the games, the method of iterated elimination of strictly dominated strategies has been used.
As an experimental feature, on can exercise the controversial method of iterated elimination of Pareto-dominated strategies as well (eliminating weakly dominated strategies).
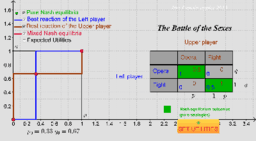
The second applet considers 2x2 bi-matrices.
The applet calculates Nash equilibria both of pure and of mixed strategies. Corresponding expected utilities can be studied.
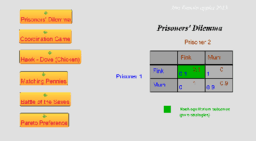
The third applet considers famous games of two players with two strategies (2x2 bi-matrices):
- Prisoners' Dilemma
- The Coordination Game
- Hawk - Dove ("Chicken")
- The Battle of the Sexes
- Matching the Pennies
One less known game with Pareto-dominated strategies has been added to illustrate the possibility of infinitely many Nash equilibria of mixed strategies.
In all of the applets, I have tried to use dynamic colours to make the tables and figures more easily readable.