Ajudar a argumentar
Com ajudar a l’alumnat a argumentar que en el lloc on la suma de distancies a cada població es mínima, es formen angles de 120º?. Mou el punt P
La situació la va plantejar Núria Guitart Francàs, del CEIP Guilleries de Sant Hilari Sacalm als seus alumnes de 6è de primària
•L’empresa “biomassa LA SELVA” vol muntar una planta d’elaboració de pellets entre els
pobles de Sant Hilari, Arbúcies i Santa Coloma.
•Us trobeu els representants dels Ajuntaments dels tres municipis i el representant
de l’empresa.
•Repartiu-vos els papers i a partir del mapa de la comarca de la Selva, feu una proposta
d’ubicació de la planta de biomassa. Prepareu un dibuix explicatiu per a la
posada en comú, escriviu els acords a que heu arribat i els arguments que han
sorgit
•Es presenta la localització al tècnic d’obres públiques de la Diputació, a fi de
que subvencioni la construcció d’accessos, però diu als municipis que tenen que
cercar una altre localització de manera que els km d’accessos sigui el mimin possible
•Com localitzar la nova situació?
Implementació de Rafa
La Y asturiana de Rafael Losada <https://www.geogebra.org/m/h2vxugnr>
Rectificar la Y
L'aeroport conjunt_ Bon dia mates_C8

Construcció
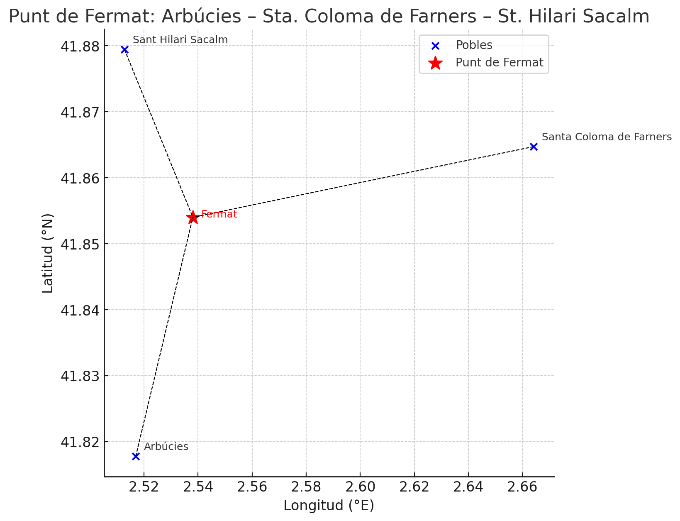
El problema: Tenim tres pobles: Arbúcies, Santa Coloma i Sant Hilari.
Volem posar un nou lloc de trobada (per exemple, una pista de joc o un parc) que estigui el més a prop possible dels tres pobles alhora.
Com podem imaginar-ho?
Corda elàstica:
Imagina que des de cada poble surt una corda elàstica que arriba al punt de trobada.
Si el punt està massa a prop d’un poble, aquella corda estira molt fort i desequilibra les altres.
Si el punt està massa a prop d’un altre poble, passa el mateix.
El punt just és aquell on les tres cordes estiren amb la mateixa força i ningú guanya.
L’equilibri
Quan les cordes estiren totes igual, es col·loquen de manera que fan el mateix angle entre elles.
Si hi ha tres cordes, l’única manera que quedin equilibrades és que cadascuna formi 120° amb les altres.
Això és com quan tens tres nens jugant a estirar d’una corda en tres direccions diferents:
Si dos estan massa junts, guanyen i el tercer cau.
Si es posen ben separats (com un triangle), ningú guanya.
El punt òptim
Aquest punt s’anomena Punt de Fermat.
És el lloc on la suma de les distàncies als tres pobles és la més petita possible.
Si el mous una mica cap a qualsevol costat, les cordes deixen d’estar equilibrades i la suma de distàncies augmenta.
Per això és com un punt d’equilibri perfecte.
Podem dibuixar-ho com un triangle amb tres cordes que es troben en un punt al mig, totes fent el mateix angle.
Sobre cada costat del triangle original es construeix un triangle equilàter cap a l’exterior.
S’uneixen els vèrtexs externs dels triangles equilàters amb els vèrtexs oposats del triangle original. Les tres rectes es tallen en un punt comú: aquest és el punt de Fermat.
Caracterització angular
El punt es pot trobar buscant aquell on els vectors que uneixen el punt amb cada vèrtex formen angles de 120°. És a dir, el punt on les forces exercides des de cada vèrtex serien equilibrades.
Matemàticament, és el punt que minimitza la suma de distàncies, i numèricament s’ha calculat amb coordenades GPS, obtenint el punt. Això assegura que cap petit desplaçament pugui millorar la suma, ja que les forces o derivades direccionals s’equilibren perfectament. Imagina que col·loquem tres cordes elàstiques que uneixen el punt PPP amb cadascuna de les tres poblacions.
Si P està massa a prop d’una població, aquella corda “estira” fortament i desequilibra el sistema.
El punt òptim és aquell on la força total és zero: el sistema queda en equilibri.
https://chatgpt.com/c/68a82197-9484-8329-b20e-736652b535ba
https://chat.deepseek.com/a/chat/s/e8113820-fcc8-482b-91c4-6cc65de793c6

