Circumcenter Exploration
A circumcenter is the point of concurrency of the three perpendicular bisectors.
1) Triangle XYZ has been constructed for you.
2) Construct the perpendicular bisector of each side using the 
tool. for example to bisect side XY, click on the tool, then click on side XY.
3) Use the intersect 
in the point menu to mark the point where all three perpendicular bisectors meet. Mathematicians call this the circumcenter . Right click this point and rename it A.
tool. for example to bisect side XY, click on the tool, then click on side XY.
3) Use the intersect in the point menu to mark the point where all three perpendicular bisectors meet. Mathematicians call this the circumcenter . Right click this point and rename it A.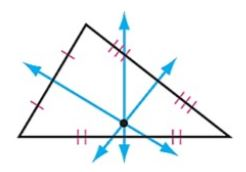
Construct the circumcenter below.
Drag the vertices of XYZ around. What kind of triangle is XYZ if the circumcenter A falls on the exterior of the triangle?
What kind of triangle is XYZ if the circumcenter A falls on the triangle?
What kind of triangle is XYZ if the circumcenter A is in the interior of the triangle?
A circumscribed circle (circle that goes through each vertex) can be added in this construction above.
Use the circle tool (
) to make a circle with the center at the circumcenter (point where all the perp. bisectors meet) and that goes through one of the vertices of the triangle.
) to make a circle with the center at the circumcenter (point where all the perp. bisectors meet) and that goes through one of the vertices of the triangle.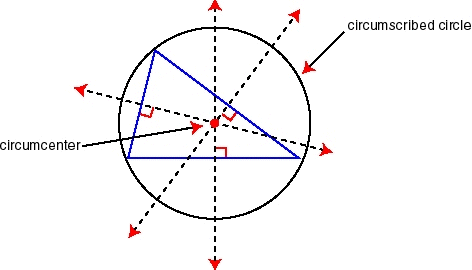
Drag around the vertices of XYZ. Does the circle always go through the three vertices and remain outside the triangle?
Since a circumscribed circle goes through each vertex, the circumcenter is equidistant from each: