Para resolver integrales por substitución... Primera parte
Comenzaremos por poner un poco de atención al símbolo que presentamos a continuación...
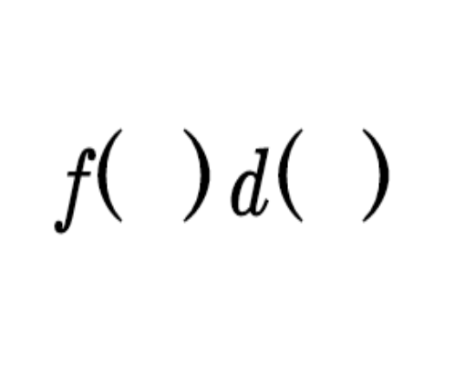
Veamos...
Es fundamental leerlo pensando en las partes que lo componen:
 Este símbolo, nos va a sugerir la forma de escribir ciertas expresiones para poder "obtener" sus integrales...
Este símbolo, nos va a sugerir la forma de escribir ciertas expresiones para poder "obtener" sus integrales...
Lo primero... las integrales básicas...
La siguiente tabla, una pequeña por cierto, la usaremos para ilustrar la importancia del símbolo que abre esta hoja de trabajo GeoGebra...Pongamos en práctica nuestra capacidad de abstraer y hacer analogías...
La siguiente expresión
¿Esta escrita de forma análoga al símbolo mencionado?
Explique por qué...
¿De dónde viene esta forma particular de escribir una expresión?
La forma expresada en la imagen del comienzo de esta hoja, está muy relacionada con la noción de la regla de la cadena...
Si miramos con atención, podremos observar como de la regla de la cadena proviene esta idea de derivar "desde la función más externa hacia la más interna"... veamos...

Observa la expresión anterior y responde...
Identifica cuál de las funciones en la expresión de arriba juega el papel de la "f" en la expresión:
Una vez identificada "f" ¿Puede decir cómo se relacionan los restantes elementos de la expresión?