Úvod
Odkazy:
Úvodní pojmy:
Hippokratés z Chiu se v rámci hledání řešení kvadratury kruhu (nalezení eukleidovské konstrukce čtverce - přesněji jeho strany - který má stejný obsah jako daný kruh) zabýval možnostmi kvadratury speciálních zakřivených útvarů - měsíčků (menisků). Měsíček je útvar vytvořený dvěma kruhovými oblouky:
Měsíčků existuje nekonečně mnoho - v závislosti na velikostech poloměrů a vzdálenosti středů obou kružnic (a tedy na úhlech a ). Avšak jejich KVADRATURU lze provést pouze pro 5 vhodných kombinací čísel , , , . To, že těchto možností je pouze 5, bylo dokázáno až ve 20. století. Avšak všech 5 možností už bylo objeveno dříve. Sám Hippokrates objevil 3 měsíčky, jejichž kvadraturu lze provést a zbylé 2 měsíčky byly objeveny v až v 18. a 19. století.
5 vhodných kombinací:
Lze dokázat, že měsíček, jehož kvadratura je možná, musí splňovat 2 podmínky:
- Poměr úhlů ku (označme ho ) musí být roven opačnému poměru druhých mocnin příslušných poloměrů, tedy:
- Poměr může nabývat pouze jedné z pěti hodnot: ; ; ; a (První tři odpovídají měsíčkům Hippokratovým)
- Ve všech pěti případech je tedy možné převést měsíček na čtyřúhelník ABCD (ve tvaru šipky jako zde - pro menší než úhel pravý) nebo ve tvaru rovnoramenného trojúhelníku (pro) či ve tvaru draka - pro větší než je úhel pravý). Ale každý mnohoúhelník lze převést eukleidovsky na čtverec a tím dokončit kvadraturu.
- V každém z pěti případů kvadratury měsíčku navíc existuje ještě další mnohoúhelník, jehož obsah je roven obsahu měsíčku - to uvidíme dále.
Základní Hippokratovo východisko - kruhové úseče:
Podobnost: Dvě kruhové úseče (resp. výseče nebo jen oblouky) jsou podobné, právě když mají stejný středový úhel.
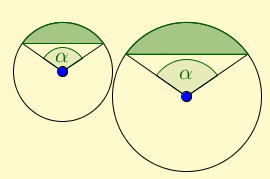
Tvrzení: Poměr obsahů dvou podobných kruhových úsečí je roven poměru obsahů čtverců sestrojených nad jejich tětivami. (Platí i pro výseče.)