The Great Pyramid

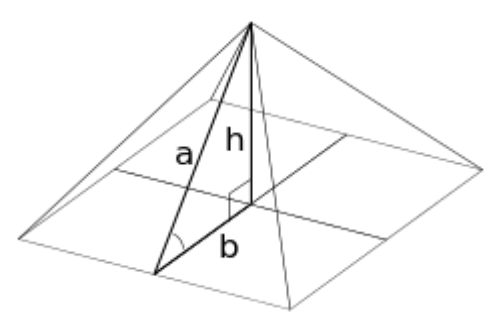
A builder wants to build an exact replica of the largest Egyptian Pyramid with the hight of 15 feet. Due to a lack of information, he only found the height and the slope of one of the faces. He assumed the structure is a right, square pyramid. The height of the pyramid is 480.69 feet and the slope of one of the faces is about . The builder wants to know the dimensions and the volume of the similar pyramid.
In order to find the apothem of the pyramid, the builder needs to use the tan ratio.
tan(51.54) =
1.258 =
= x
x 382.11
The apothem of the pyramid is about 382.11 feet.
Because he knows that this is a right, square pyramid, all he has to do to find one missing side length is multiply the apothem by two.
-
= 764.22
The side length is 764.22 feet
V = Bh
V = (764.22)(764.22)(480.69)
V 93,579,480.75 feet
The volume of the larger pyramid is about 93,579,480.75 feetTo find the scale factor, divide the height of the smaller pyramid to the larger pyramid.
= scale factor
0.031 scale factor
To find one of the side lengths of the base, multiply the side length of the actual pyramid's base to the scale factor.
764.22 0.031 23.69
The dimension of one of the side lengths of the smaller pyramid's base is about 23.69 feet
To find the volume of the smaller pyramid, he needs to cube the scale factor and make the proportion below.
= 0.031
= 0.00003
x 2,807.38 feet
The volume of the smaller pyramid is about 2,807.38 feet
Picture Citations
First picture: http://famouswonders.com/great-pyramids-of-giza/
Second picture: https://en.wikipedia.org/wiki/Golden_ratio#Golden_ratio_conjugate