Attività 1: Poligoni regolari
[G 134 sul libro]
Definizione Un poligono è regolare quando ha tutti i lati congruenti e tutti gli angoli congruenti.
Come costruire un poligono regolare: possiamo utilizzare il comando di Geogebra  oppure seguire la costruzione che vedremo fra poco.
Teorema Un poligono regolare è inscrivibile in una circonferenza e circoscrivibile a un'altra; le due circonferenze hanno lo stesso centro.
Utilizziamo Geogebra per una traccia della dimostrazione.
oppure seguire la costruzione che vedremo fra poco.
Teorema Un poligono regolare è inscrivibile in una circonferenza e circoscrivibile a un'altra; le due circonferenze hanno lo stesso centro.
Utilizziamo Geogebra per una traccia della dimostrazione.
 oppure seguire la costruzione che vedremo fra poco.
Teorema Un poligono regolare è inscrivibile in una circonferenza e circoscrivibile a un'altra; le due circonferenze hanno lo stesso centro.
Utilizziamo Geogebra per una traccia della dimostrazione.
oppure seguire la costruzione che vedremo fra poco.
Teorema Un poligono regolare è inscrivibile in una circonferenza e circoscrivibile a un'altra; le due circonferenze hanno lo stesso centro.
Utilizziamo Geogebra per una traccia della dimostrazione.
- disegniamo un pentagono regolare
 , ma la dimostrazione può essere generalizzata
, ma la dimostrazione può essere generalizzata
- tracciamo le bisettrici
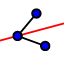 dell'angolo A e dell'angolo B. Indichiamo con O il punto di intersezione. Congiungiamo OC.
dell'angolo A e dell'angolo B. Indichiamo con O il punto di intersezione. Congiungiamo OC.
- Verifichiamo che OC è bisettrice, ad esempio misurando gli angoli BCO e OCD
- Congiungiamo il punto O con i rimanenti vertici e osserviamo che tali segmenti sono bisettrici di ciascun degli angoli al vertice. Otteniamo tutti triangoli isosceli fra loro congruenti
- Il punto O è equidistante da tutti i vertici del poligono e rappresenta il centro della circonferenza in cui il poligono è inscritto
- Il punto O è anche il punto di icontro di tutte le bisettrici e dunque è equidistante da tutti i lati del poligono (per la proprietà della bisettrice). Quindi il punto O rappresenta il centro della circonferenza alla quale il poligono è circoscritto.
Elementi notevoli di un poligono regolare:
- il centro è il centro delle circonferenze inscritta e circoscritta;
- l'apotema è il raggio della circonferenza inscritta;
- il raggio è il raggio della circonferenza circoscritta.