Cálculo de áreas: integrales definidas
1. Introducción: funciones positivas
Sea una función , es decir, definida en un intervalo. Supongamos que es positiva, es decir, que (su gráfica está por encima del eje de abscisas). Entonces, la integral definida
representa el área encerrada entre la gráfica de y el eje de abscisas entre las rectas y .
Por ejemplo, si la función es y y , tenemos que el área coloreada de amarillo
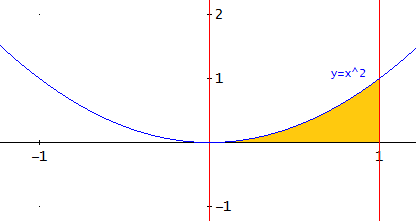
es
es
2. Funciones negativas
Supongamos ahora que la función es negativa en el intervalo, es decir, que . En este caso, la integral definida nos proporciona el área pero, al estar la región por debajo del eje de las abscisas, la integral proporciona un valor negativo. Lo único que tenemos que hacer es cambiar el signo del resultado, es decir, calcular el valor absoluto. Por ejemplo, si cambiamos la función por , el área será Obviamente obtenemos el mismo valor ya que se trata de la misma región tras aplicar una simetría respecto del eje OX.
3. Funciones de signo no constante
Ahora consideramos la posibilidad de que la función no sea siempre positiva ni negativa, esto es, existen algunos intervalos en los que la función es positiva y otros en los que es negativo (si la función es 0, no importa si la consideramos positiva o negativa).
Lo que hacemos en estos casos es calcular el área de las regiones asociadas a cada intervalo: en los intervalos en los que la función es positiva, calculamos la integral definida de la función; en los que es negativa, calculamos la integral definida de la función y cambiamos el signo.
Finalmente, sumamos las áreas para obtener el área total.
Por ejemplo, vamos a calcular el área de la función en el intervalo . Es fácil ver que la función es positiva en el intervalo y negativa en el intervalo . Luego tendremos dos integrales.
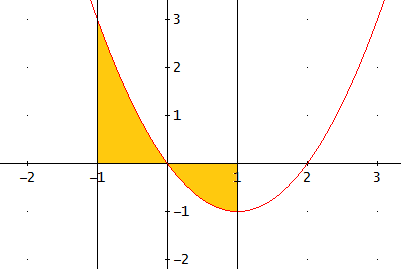
El área donde la función es positiva es
El área donde la función es negativa es:
Por tanto, el área total es
El área donde la función es positiva es
El área donde la función es negativa es:
Por tanto, el área total es
4. Área entre las gráficas de dos funciones
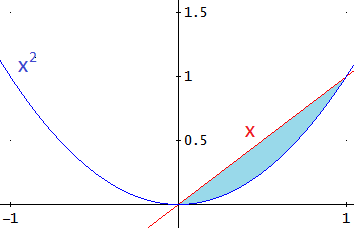
siendo , , y .
Es fácil ver que el área a la que nos referimos la podemos obtener como el área que hay entre la gráfica de y el eje de abscisas menos el área que hay entre la gráfica de y el eje de abscisas. Esto es,
el área que buscamos es
Podemos encontrarnos en casos mixtos, por ejemplo: intervalos en los que ambas gráficas tienen el mismo signo, intervalos en los que no tienen el mismo signo, intervalos en los que es mayor una función que la otra...
Para poder calcular el área total tendremos que descomponerla, de forma análoga a como lo hicimos anteriormente, en varias integrales.
siendo , , y .
Es fácil ver que el área a la que nos referimos la podemos obtener como el área que hay entre la gráfica de y el eje de abscisas menos el área que hay entre la gráfica de y el eje de abscisas. Esto es,
el área que buscamos es
Podemos encontrarnos en casos mixtos, por ejemplo: intervalos en los que ambas gráficas tienen el mismo signo, intervalos en los que no tienen el mismo signo, intervalos en los que es mayor una función que la otra...
Para poder calcular el área total tendremos que descomponerla, de forma análoga a como lo hicimos anteriormente, en varias integrales.