Kapitel
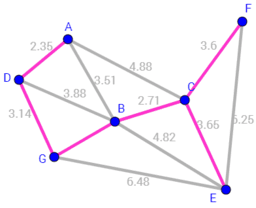
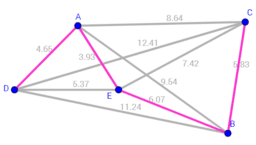
Minimal Spanning Tree
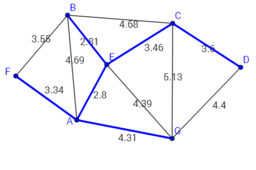
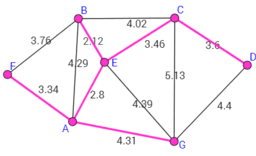
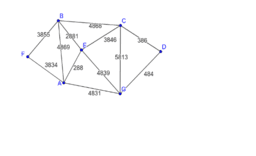
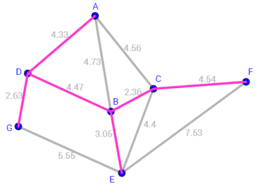
A minimum spanning tree (MST)[/b] is a subset of the edges of a connected, edge-weighted (un)directed graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible.
