El centro del círculo que corta un triángulo proporcionalmente
- Autor:
- Rafael Losada Liste
- Tema(s):
- Circunferencia, Construcciones, Geometría, Triángulos
Esta actividad pertenece al libro de GeoGebra Color dinámico.
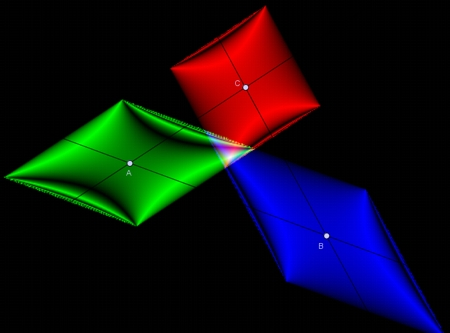
Veamos otro ejemplo de barrido automático. Sea el triángulo de vértices A, B y C Queremos encontrar los puntos en donde situar el centro de un círculo de radio dado para que corte a esos lados (o sus prolongaciones) en cuerdas proporcionales a sus longitudes.
Obtenemos una imagen que nos muestra que tal punto es la intersección de tres hipérbolas (roja, verde y azul) que pasan por los vértices de rombos centrados en los vértices.
Se busca el centro (variable) B1 de la circunferencia de radio fijo r de forma que la circunferencia corte a los lados en cuerdas proporcionales a sus longitudes.
Para ello, definimos las constantes:
r = 2
d = Recta[A, B]
f = Recta[B, C]
g = Recta[C, A]
AB = Segmento[A, B]
BC = Segmento[B, C]
CA = Segmento[C, A]
y las variables:
C1 = Circunferencia[B1, r]
D1 = Distancia[Interseca[C1, d, 1], Interseca[C1, d, 2]]
E1 = Distancia[Interseca[C1, f, 1], Interseca[C1, f, 2]]
F1 = Distancia[Interseca[C1, g, 1], Interseca[C1, g, 2]]
Así que el código de color dinámico es:
R = E1 CA / (F1 BC)
G = F1 AB / (D1 CA)
B = D1 BC / (E1 AB)
Pulsa el botón de Reproducción (esquina inferior izquierda) para activar el escáner.
Autor de la actividad y construcción GeoGebra: Rafael Losada.