the problem of the diagonal
the problem of the diagonal
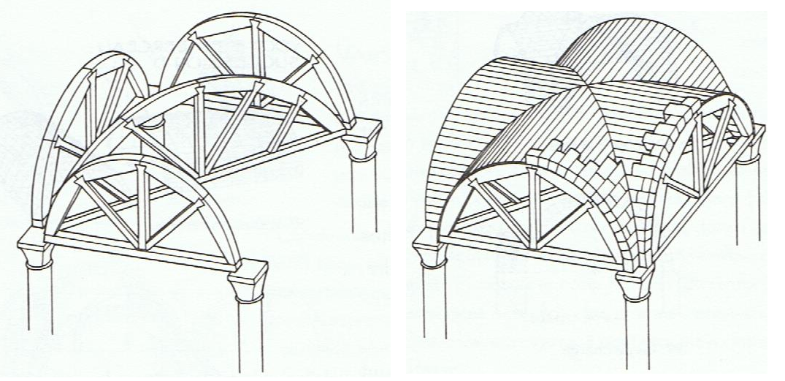
A barrel vault is circular and that's ok since circular arcs are self supporting. The story becomes different if you make the intersection of two crosswise placed barrel vaults. When rotating the applet, you can see that the intersecting line stands upon the diagonal of a square. Since the height of it equals the side of the square, the resulting arc is too low to be circular.
Geometrically this is normal: the diagonal of a square is longer than its side. But in a construction it's problematic since the intersection of the vaults is the most important line in the groined vault and should be circular.
building groined vaults
During the building process vaults were supported by wooden foldings. To construct them, they were drawn on the floor livesize, using ropes as compasses. Not circular arc were problamatic constructively, but moreover is was difficult to draw them.