Reflection
A reflection is a transformation that uses a line like a mirror to reflect or "flip" a figure. The mirror line is called the "line of reflection."
The following activities will help you explore various types of reflections. Like the last exploration, observe how this type of transformation affects the points, segments and angle measures of the figure when creating the image.
Reflection over the y-axis (x = 0) (After exploring, answer #1)
Reflection over the x-axis (y = 0) (After exploring answer #2)
Reflection over a vertical line (After exploring, answer #3)
Reflection over a horizontal line (After exploring answer #4)
Reflecting over the line y=x (After exploring answer #5)
Other Relationships within Reflections
Return to the above GeoGebra sketches. Add lines connecting the original point to its image. Notice the relationship between these lines and the line of reflection. Add your thoughts to question #6.
Guess the equation of the reflection line used to create this image. Record your answer in #7.
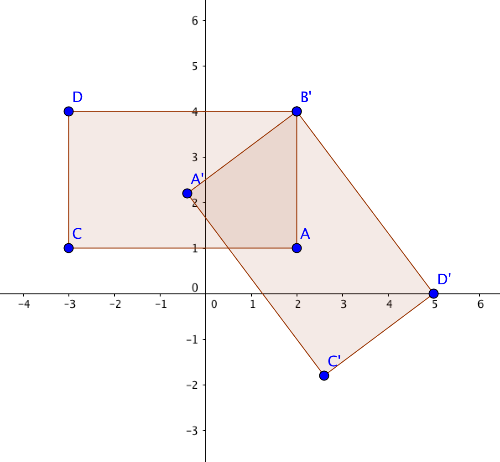
Use the input bar to insert your guess for the line of reflection into the sketch. Then, use the GeoGebra tools to check the accuracy of your line. Record how close your guess was to the actual and what the actual equation in #8.
Reflection Rules
So far you have explored three different scenarios. You should have noticed the following patterns or rules: If a figure is reflected in the y-axis, then all of the points will move according to the rule . If a figure is reflected in the x-axis, then all of the points will move according to the rule . If a figure is reflected in the line y = x , the all of the points will move according to the rule . What do you think is the rule when figures are reflected in the line y=-x? (Record your answer in 9)
Challenge 1
Explore what happens when we perform a composition of two reflections. Return to one of the sketches above. Add a second line of reflection. Use the "reflect about a line" tool to reflect the image again.
Record the summary of your observations below in #10.
Challenge 2
Explore what happens when we do a composition of a translation and reflection. Use the sketch below to add a vector and a line of symmetry. Explore performing a translation, then a reflection and a reflection, then translation. Does the order matter?
This type of transformation (or composition of transformations) is called a Glide Reflection.
What did you observation about Glide Reflections? (Record in #11)
Can you do it on your own?
Create a line of reflection using the line tool. Then use the "reflect about a line" tool to create the image.