Exploring Right Triangles
First you will need to pick an angle between 0 degrees and 45 degrees that is a multiple of 5. Write your angle below.
Use the slider to dial in a triangle that has your angle. Then use point A to change the size of the triangle. Write down the side lengths of the legs adjacent to your angle and opposite to your angle for five different-sized triangles. Then calculate the ratio of the opposite side over the adjacent side for each triangle.
What is true about the ratios you found above? Explain why this makes sense geometrically.
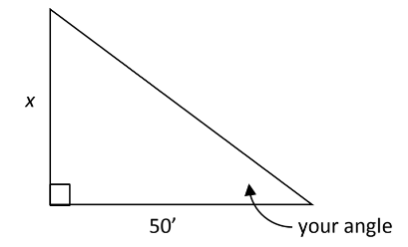
Consider a situation where a person is standing 50' away from a building. The angle between the ground and the line that goes to the top of the building is the same as your angle above. Find the height of the building. Show how this could be calculated using the ratio from above.
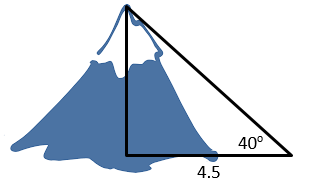
A mapmaker stands 4.5 miles away from the center of a mountain. She uses an instrument called a sextant to site the angle of elevation to the top of the mountain at 40o. What is the height of the mountain? Show work. (The ratio of opposite/adjacent for 40 degrees is 0.839)
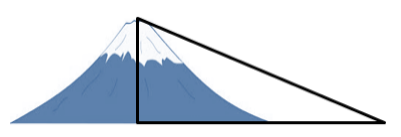
The mapmaker travels to a new location with a different mountain. She knows that this new mountain is 15,000 feet tall. From her vantage point, the angle of elevation to the top of the mountain is 25o. How far away from the center of the mountain is she standing? Show work. (The ratio of opposite/adjacent for 25 degrees is 0.446)