Lugares geométricos 5
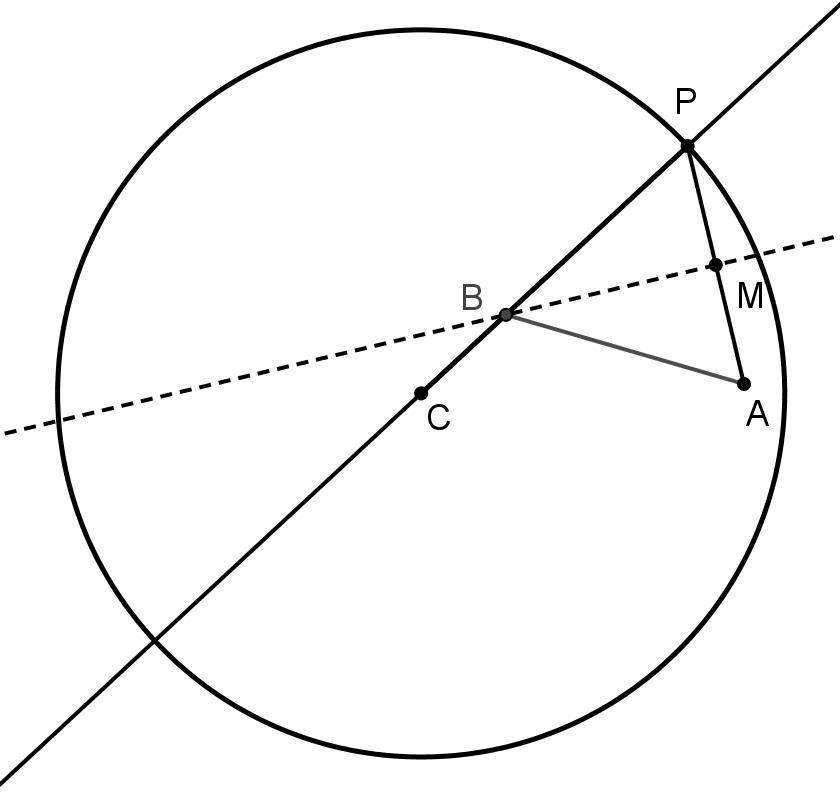
Figura 1
Applet 1
a) Arrastre el punto P sobre la circunferencia y haga una lista con las cantidades que permanecen constantes durante este movimiento.
b) Identifique aquellas cantidades que varían al arrastrar P y haga otra lista con ellas.
c) De las cantidades de la lista anterior, identifique aquellas que aunque varían al arrastrar P, permanecen iguales entre sí.
d) Al arrastrar el punto P, ¿la cantidad CB + BA varía o permanece constante? Justifique su afirmación.
e) Utilice la herramienta “Lugar geométrico” para obtener la curva que describe el punto B, cuando el punto P se mueve sobre la circunferencia. ¿A qué curva corresponde el lugar geométrico obtenido? Ofrezca una explicación geométrica de su respuesta.
f) ¿Qué relación tienen ahora los puntos A y C con la nueva curva obtenida? Justifique su respuesta.
a) ¿En qué curva se transformó su lugar geométrico? Ofrezca una explicación geométrica de su respuesta.
b) P. ¿Qué relación tienen ahora los puntos A y C con la nueva curva trazada? Justifique su respuesta.
Applet 2
a) Cuando el punto P se mueva, las distancias CB y AB cambiarán, pero la suma CB+AB permanecerá constante e igual a 5, como se ha visto antes. Use la fórmula para expresar las distancias CB y AB en términos de x y y. Para que el punto B permanezca sobre la elipse, debe satisfacer la condición: CB+AB = 5 Use las expresiones algebraicas encontradas para expresar la ecuación anterior en términos de x y y. Luego simplifique la ecuación todo lo que pueda y escriba la versión simplificada
Figura 2
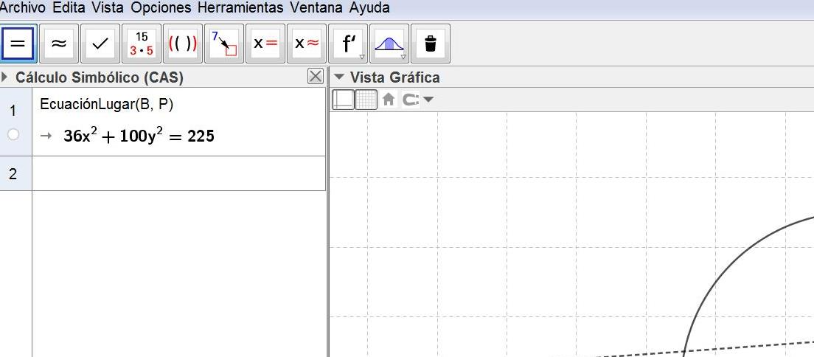
Compare este resultado con la simplificación de la ecuación que obtuvo en el inciso anterior y en su caso comente las diferencias que observa.
c) En la ecuación haga y=0 y despeje x en la ecuación obtenida para calcular las intersecciones de la curva con el eje X. Compare las intesecciones obtenidas con la gráfica que se muestra en el Applet 2 que ha descargado y escriba aquí sus conclusiones
d) En el Applet 2 descargado arrastre el punto A, hasta que sus coordenadas sean (4,0). La curva que traza el punto B ahora es una hipérbola. Investigue la definición de hipérbola y escríbala aquí con sus propias palabras.
e) De acuerdo con la definición de hipérbola, para que un punto B trace la curva de la figura anterior debe cumplir con la condición siguiente: |CB-AB|=5 lo cual significa que CB-AB=5 o bien que CB-AB=-5, cada una de estas ecuaciones representa una rama de la hipérbola. Al igual que en el caso de la elipse, si queremos obtener la representación algebraica de la hipérbola, podemos usar la fórmula de la distancia entre dos puntos y sustituir las expresiones, por ejemplo en la ecuación: CB-AB=5 Haga las sustituciones y simplifique la ecuación resultante.
Figura 3
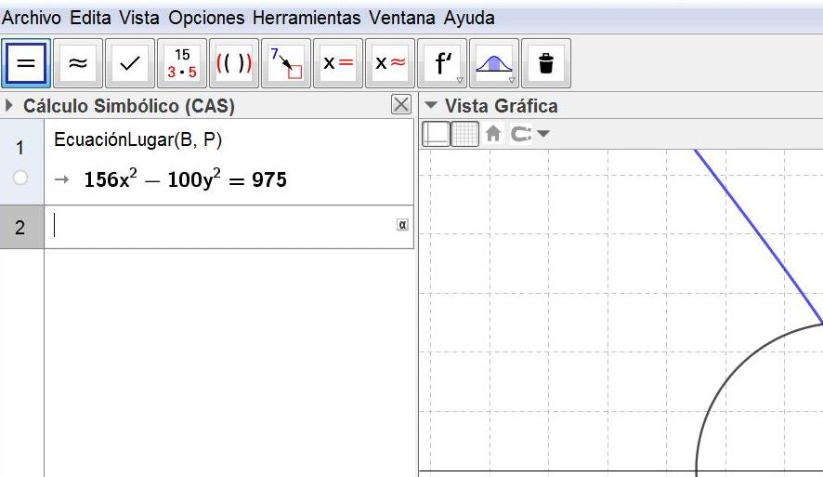
Compare su simplificación con la ecuación del lugar geométrico calculado por GeoGebra, ¿son equivalentes?
g) En la ecuación haga y=0 y despeje x en la ecuación obtenida para calcular las intersecciones de la curva con el eje X. Compare las intesecciones obtenidas con la gráfica que muestra el Applet 2, escriba aquí sus conclusiones.
h) En la ecuación haga x=0 y despeje y en la ecuación obtenida para calcular las intersecciones de la curva con el eje Y. Explique por qué la ecuación no tiene soluciones reales y use el Applet 2 para explicar lo que significa gráficamente la inexistencia de soluciones reales para esta ecuación.