cilinder in kegel
In een kegel met straal 4cm en een hoogte van 6cm plaats je een cilinder.
Voor welke afmetingen wordt de inhoud van de cilinder maximaal?
De straal van de kegel = |AD| = 4cm
De hoogte van de kegel = |DE| = 6cm
Wanneer we de straal van de cilinder x noemen,
kunnen we de hoogte uitdrukken in functie van deze straal
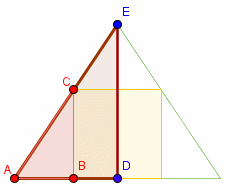De cilinder bepaalt twee gelijkvormige driehoeken: ΔABC en ΔADE.
Hierin vinden we volgende gelijkheid :
voor |AD| = 4 en |BD|=x wordt |AB|= 4 - x, zodat:
h = 1,5. (4 - x)
h = 6 - 1,5x
De inhoud van een cilinder vinden we als I = π r2 . h
We krijgen dus:
I (x) = π x2 . (6 - 1,5x)
I (x) = 6π x2 - 1,5π x3
De inhoud wordt maximaal als I ' (x) = 0
I ' (x) = 12 π x - 4,5 π x2 = 0
π x (12 - 4,5 x) = 0
nulpunten zijn x = 0cm en x = 8/3 (2,67)cm.
De inhoud van de cilinder zal maximaal zijn voor een straal van 2,67cm.
De hoogte van de cilinder is dan 6 - 1,5x = 6 - 1,5. 2,67 = 2 cm
De cilinder bepaalt twee gelijkvormige driehoeken: ΔABC en ΔADE.
Hierin vinden we volgende gelijkheid :
| |CB| | = |ED| | |
| |AB| | |AD| |
| h | = 6 | |
| 4 - x | 4 |