MthEd608FinalNatascha3a
Question 3
a) The student conjectured that every time , the number of rectangles in the interval doubles, the difference between the upper and lower sums halves. After exploring the applet below by experimenting with different functions and number of rectangle divisions, the student's conjecture seems to be true when the function is a polynomial, logarithmic, or a polynomial. This is because for any of these functions if represents the height of the rectangle in the lower summer it is also the height of the rectangle in the upper sum if is decreasing and the if is increasing. Furthermore, if we are finding the area beneath on the bound , then the width of each rectangle is . Thus the area of each rectangle within would be . However, since each area would be repeated for the upper and lower sum, when the two areas are subtracted and after factoring we would get the difference of the upper and lower sums, excluding the would points would be 0. Thus, the difference between the upper and lower sums will be difference between the areas at the points: . If we double the number of rectangles, than the width of each rectangle is halved, or and the area will be , have of what it was when there were rectangles.
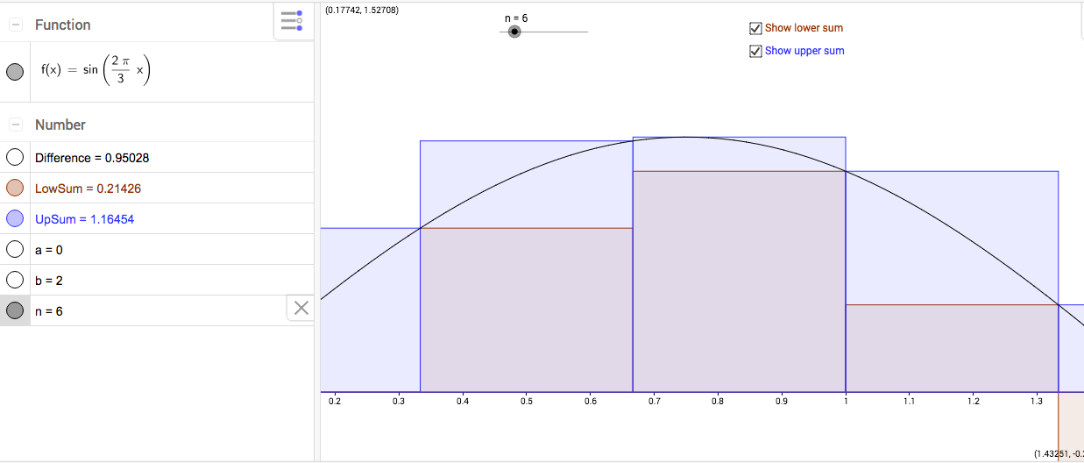
b)This proof, however, does not work for graphs where the left and right hand sums are not always the upper and lower limits, for example or or any related functions. I came to this conclusion by using the applet below. When experimenting with sine and cosine functions, I discovered that when changing from two to four rectangles, the difference between the upper and lower sums remains them sum. Furthermore, some some doublings resulted in something close to halving the difference between the upper and lower sums, but not exactly. At first, I thought that if I adjusted the period so that the width of the given interval was one period, the pattern of halving the difference between the upper and lower sums when doubling the number of rectangles would hold. However, it did not. This led me to look closer at the rectangles. While the other functions used exclusively left and right hand sums to estimate, the rectangles on the sine and cosine curve were not always left and right hand sums. (See the picture below for an example). Thus, the heights of the rectangles are not always the same for the upper and lower sums and the middle terms will not always cancel out exactly. Therefore, the difference between the upper and lower sums will not always be halved when the number of rectangles is doubled.
MthEd608Final6b