Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

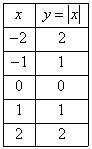
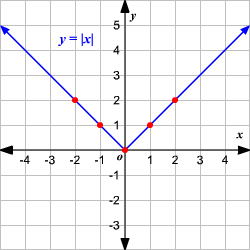
Gráfica Función Valor Absoluto

Autor:luisvegab
Antes de hablar de Gráfica de la Función Valor Absoluto, Recordemos que la definición del Valor Absoluto surge de nociones geométricas, y se relaciona con los conceptos de longitud y distancia. En palabras más simple, es a qué distancia hay de un número a cero:
Image
La función de valor absoluto tiene por ecuación , está definida como:
Para graficar la Función Valor Absoluto, se hace de manera tabular dándole valores a "X" , encontrando los valores de "Y" para obtener los valores coordenados. Por ejemplo:
Una vez encontrado los valores coordenados, se grafican los puntos y se unen como representa la gráfica.
El Objetivo de esta clase es aprender a graficar la función Valor absoluto y discriminar su gráfica según corresponda a cada ecuación sin datos tabulados, con ayuda del software Geogebra. A continuación la gráfica que se presenta en la ventana de geogebra serás protagonista de tu aprendizaje al ver cómo se comporta la Gráfica de Función Valor Absoluto usando deslizadores. Para ello, es necesario que al presionar el recuadro del "tiket" de la función , utilice el deslizador para ver cómo se comporta la función dada la ecuación. Luego para presionar click en el recuadro recuadro de la función , deberá quitar el "tiket" de la función anterior para visualizar de manera efectiva el comportamiento de la función utilizando el deslizador.
Ahora analizaremos...

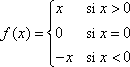
1- En la Función g(a)

¿Qué ocurre con la gráfica de la Función Valor Absoluto si hay una constante dentro del Valor Absoluto? ¿Qué ocurre si la constante es POSITIVO? ¿Qué ocurre si la constante es NEGATIVO?

2.- En la Función h(a)...

a) ¿Qué ocurre si esta constante está fuera del Valor Absoluto? b) ¿Qué ocurre si la constante es POSITIVO? c) ¿Qué ocurre si la constante es NEGATIVO?

3- En la función i(a)

a) ¿Qué provoca que el coeficiente del valor absoluto es negativo? b) ¿Cuáles son las diferencias y lo común entre las funciones g(a) y j(a)? c) ¿Cuáles son las diferencias y lo común entre las funciones h(a) y k(a)?

4-

a) ¿Qué ocurre si hacemos X=0 en cualquier función dada anteriormente?, ¿Cuál sería la coordenada? b) ¿Qué representa esa coordenada en la función?

Una vez analizado el comportamiento de cada Función de Valor Absoluto, cabe destacar el análisis de la pendiente de esta función. Para ello con Geogebra analizaremos dicho caso. En esto una vez más serás protagonista del aprendizaje, en los recuadros de cada constante (a, b y c), podrás darles valores para ver cómo se comporta la Función Valor Absoluto. (Cabe destacar que en la constante "a" puede ser un número racional, y que el valor está en [-5,5] )
Para analizar lo anterior, responde las siguientes preguntas:

1- ¿Qué sucede cuando al la constante "a" está entre los valores [1,5]?

2- ¿Qué sucede cuando al la constante "a" está entre los valores [-5,-1]?

3- ¿Qué sucede cuando al la constante "a" es 0?

Por último para Terminar la clase, retroalimentaremos lo enseñado. Como puedes ver, la Gráfica Función Valor Absoluto es mucho más simple de lo que parece, ya que no necesitamos depender de la tabla de valores para poder graficar según el tipo de Función Valor Absoluto, simplemente analizando las interrogantes propuestas anteriormente.
Para terminar dejaré de tarea el cómo quedará la gráfica según la función: . Puedes Ayudarte con la ventanilla Geogebra anterior para ingresar los valores y verificar si tu gráfica coincidió.

Nuevos recursos

Descubrir recursos

Descubre temas