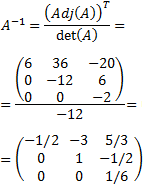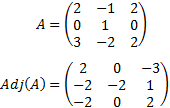Matriz inversa (a partir de la adjunta)
Introducción
Sea una matriz de dimensión y regular (su determinante es distinto de 0). Entonces, existe una matriz que llamamos inversa de A y representamos por que cumple:
- , siendo la matriz identidad de dimensión
- la matriz inversa es única. Es decir, sólo hay una matriz que cumple el punto anterior.
Transposición
Para cualquier matriz de dimensión . llamamos matriz transpuesta de y la denotamos por a la matriz que resulta al escribir las columnas de como filas de . Es decir, la fila i de es la columna i de .
Al cambiar filas por columnas, la dimensión de es .
Ejemplo
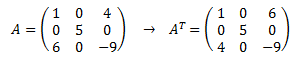
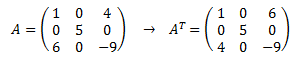
Ejemplos de matriz inversa
Ejemplo 1:

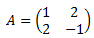 Calculamos los elementos de la adjunta de A:
Calculamos los elementos de la adjunta de A:
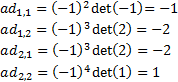
La matriz adjunta es
La matriz adjunta es
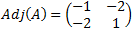
Notemos que no es necesario escribir su transpuesta ya que coinciden.
El determinante de A es
Notemos que no es necesario escribir su transpuesta ya que coinciden.
El determinante de A es
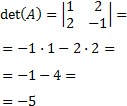
Por tanto, la inversa de A es
Por tanto, la inversa de A es
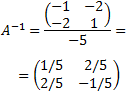
Ejemplo 2:
Ejemplo 2:

Calculamos los elementos de la adjunta:
Calculamos los elementos de la adjunta:
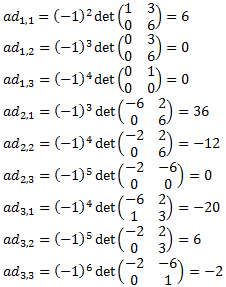
La adjunta es:
La adjunta es:
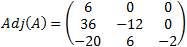
El determinante de A es
El determinante de A es
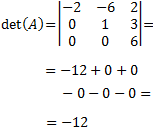
Por tanto, la inversa de A es
Por tanto, la inversa de A es
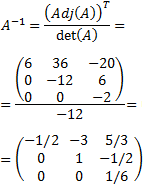

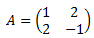 Calculamos los elementos de la adjunta de A:
Calculamos los elementos de la adjunta de A:
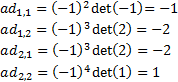
La matriz adjunta es
La matriz adjunta es
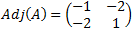
Notemos que no es necesario escribir su transpuesta ya que coinciden.
El determinante de A es
Notemos que no es necesario escribir su transpuesta ya que coinciden.
El determinante de A es
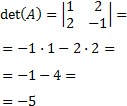
Por tanto, la inversa de A es
Por tanto, la inversa de A es
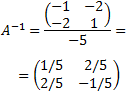
Ejemplo 2:
Ejemplo 2:

Calculamos los elementos de la adjunta:
Calculamos los elementos de la adjunta:
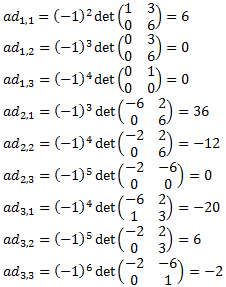
La adjunta es:
La adjunta es:
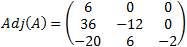
El determinante de A es
El determinante de A es
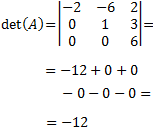
Por tanto, la inversa de A es
Por tanto, la inversa de A es