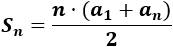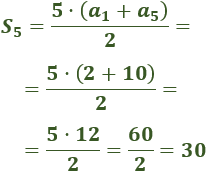Progresiones aritméticas
Introducción
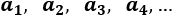
Una sucesión (o progresión) es un conjunto de números ordenados. Cada número ocupa una posición y recibe el nombre de término.
Ejemplo: Un ejemplo de sucesión es el conjunto de los números pares: 2, 4, 6, 8, 10, 12, 14,...
El término que ocupa la posición n se denota por y se denomina término general o término n-ésimo.
Ejemplo: En la sucesión de las pares, el primer término es y el sexto es . El término general es .
Una sucesión es aritmética cuando cada término se obtiene sumando un número al término que le precede. Este número se denomina diferencia y se denota por .
Una sucesión (o progresión) es un conjunto de números ordenados. Cada número ocupa una posición y recibe el nombre de término.
Ejemplo: Un ejemplo de sucesión es el conjunto de los números pares: 2, 4, 6, 8, 10, 12, 14,...
El término que ocupa la posición n se denota por y se denomina término general o término n-ésimo.
Ejemplo: En la sucesión de las pares, el primer término es y el sexto es . El término general es .
Una sucesión es aritmética cuando cada término se obtiene sumando un número al término que le precede. Este número se denomina diferencia y se denota por .
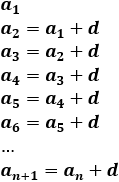 Fórmula para calcular la diferencia:
Fórmula para calcular la diferencia:
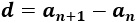 Es decir, la diferencia se obtiene restando términos consecutivos.
Si la diferencia entre dos términos consecutivos no es constante en toda la sucesión, entonces la sucesión no es aritmética.
Es decir, la diferencia se obtiene restando términos consecutivos.
Si la diferencia entre dos términos consecutivos no es constante en toda la sucesión, entonces la sucesión no es aritmética.Término general
Se puede calcular cualquier término de la sucesión mediante una fórmula (fórmula o término general). Esta fórmula se obtiene a partir del primer término y de la diferencia:
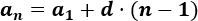
Ejemplo: Calculamos el término 10-ésimo de la sucesión de los pares.
Como el primer término es y la diferencia es , el término que ocupa la décima posición es
Ejemplo: Calculamos el término 10-ésimo de la sucesión de los pares.
Como el primer término es y la diferencia es , el término que ocupa la décima posición es
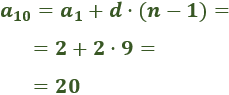
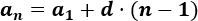
Ejemplo: Calculamos el término 10-ésimo de la sucesión de los pares.
Como el primer término es y la diferencia es , el término que ocupa la décima posición es
Ejemplo: Calculamos el término 10-ésimo de la sucesión de los pares.
Como el primer término es y la diferencia es , el término que ocupa la décima posición es
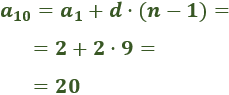
Suma de los primeros términos
Más información y problemas resueltos de sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente