Sisällysluettelo
Johdanto
Tässä muistiinpanoni lukion AT6 kurssista, Matematiikkaa tietokoneella. Laajus 12-15 oppituntia.
Suunnitelmani
1.1 Tutustutaan ohjelmaan
2.1 Liuku- kytkimen luonti
2.2 Ongelman ratkaisu CAS avulla: derivointi + derivaatannollakohdat, tekstikenttä, vapaa piirto, lisänä laTeXin alkeita
2.3 Geometrinen piirros, piirrä samanlainen. Ja vastaa kysymyksiin.
2.4 CAS opettelua, suurimman ja pienimmän arvon löytäminen.
2.5 Imaginääriset ratkaisut
2.6 Ratkaisukaavaan dynaamiset muuttujat + LaTeX
3.1 Pisteen x-koordinaatti sekä Derivaatan ymmärtäminen!?
3.2 Derivaatan arvo = tangentin kulmakerroin
3.3 Fermat’n lause
3.4 Funktion monotonisuus
3.5 Ongelman ratkaisu liittyen derivaattaan
4.1 Trigonometrisen funktion suurin ja pienin arvo
3D ongelmia, ratkaise kaikki tietokoneenavulla .
1. Kuution muotoisen pöydän päälle sijoitetaan kynttilä. Kynttilä sijoitetaan tarkalleen pöydän
keskelle. Palava kynttilä muodostaa lattialle 9x varjo kuution tahkoon nähden. Kuinka korkea on kynttilä?
2. Piirrä
a) Kuution ulkopuolellapiirretään pallo siten, että kuution kärjet ovat pallon pinnalla.
b) Kuution sisäpuolellepiirretään pallo siten, että se sivuaa kuution tahkoja
Mikä on ison pallon tilavuuden suhde pinemmän pallon tilavuuteen? Tarkka-arvo!
3. Sijoita pallon sisään suurin mahdollinen oktaedri. Mikä on oktaedrin tilavuuden suhde palloon?
4. Tennispallopyramidi! Neljä tennispalloa asetetaan pöydälle vierekkäin siten, että viides pallo voidaan sijoittaa niiden
päälle. Kuinka korkea pyramidista tulee?
5. Opetusajatus: Kuinka voisin opettaa ja perustella miksi kartion tilavuus jaetaan kolmella????
6. Kahden paikkavektorin välinen kulma?
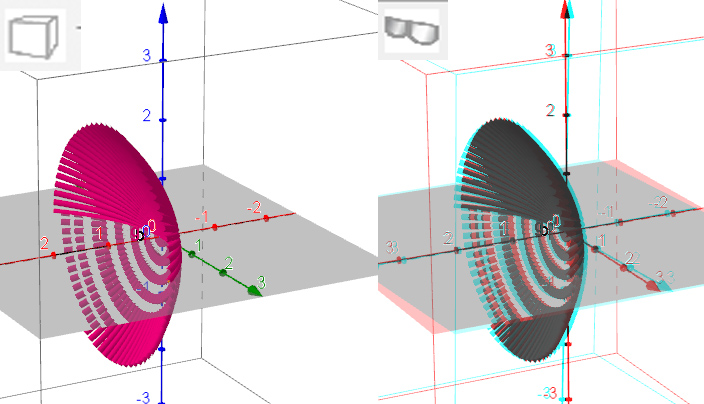
7. Pyörähdyskappale:
a) Mikä se on? Johdantona voisi näyttää 4.1 esimerkin.
b) K2015 T10. Ratkaistaan tehtävä GeoGebran avulla ja mietitään 3D vs 3d.