Klausur Nr. 1
1. Skizziere ohne Rechnung die Graphen der Funktion f und der Ableitungsfunktion f‘.
a) b)
2. Bestimme die ersten beiden Ableitungen
a) b)
3. Ein Herd wird zum Backen vorgeheizt, bis er eine vorgeschriebene Endtemperatur erreicht hat. Die Temperatur im Herd (in °C) in Abhängigkeit von der Zeit t (in Minuten) kann durch eine Funktion T beschrieben werden.
a) Skizziere einen möglichen Graphen von T. (Markiere dazu ca. 5 - 10 Punkte in Geogebra, der den Verlauf deutlich darstellt.)
b) Welches Vorzeichen hat T‘?
c) Interpretiere die Aussagen: T(5) = 80 und T‘(10) = 2
d) Was bedeutet: T(6) – T(5) = 20
Der Temperaturunterschied zwischen der 5. und 6. min beträgt 20°
4. Die Abbildung zeigt die Graphen der beiden Funktionen f und g.
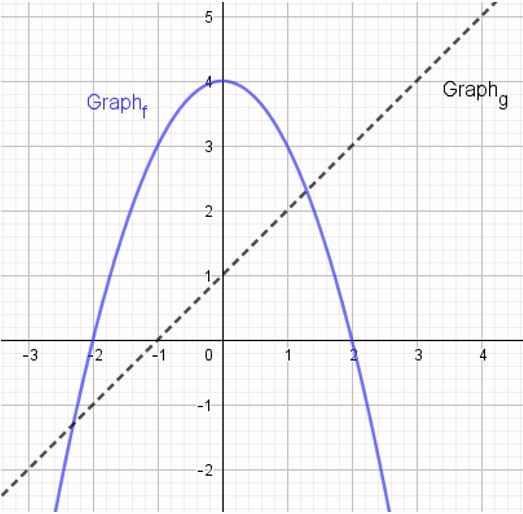
a) Bestimme (f°g)(0) und (g°f)(0) b) Gibt es Werte von x, sodass (f°g)(x)=0 ist?
5. Ein Eiskunstläufer gleitet entlang einer Kurve mit der Gleichung
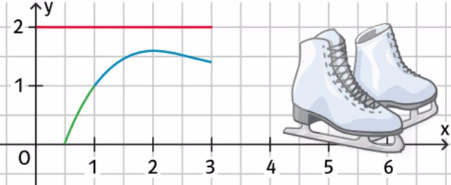
a) Berechne die Koordinaten des Punktes A, an dem er an der Bande aufprallt.
b) Zwei unerfahrene Läufer begegnen sich auf dem Eis.
Läufer A fährt entlang der Kurve der Funktion f und Läufer B entlang einer Kurve der Gleichung Sie können einen Zusammenprall gerade noch verhindern und „berühren“ sich nur im Punkt P(1|f(1)). Bestimme dazu die Koeffizienten a und c. Schreibe dazu vorher auf, was „berühren“ im mathematischen Sinn bedeutet.
6. Gegeben ist die Funktion f mit
a) Bilde die erste Ableitung von f und fasse den Term soweit wie möglich zusammen.
b) Bestimme die Schnittpunkte des Graphen von f mit der x-Achse.
Zeige, dass die Steigungen der Tangenten an den Graphen von f in diesen Punkten die Werte m1 = und m2= -2 annehmen.
Trage die beiden Tangenten sowie f' oben in das Koordinatensystem ein.
Beschreibe hier den Rechenweg.