Le formule di bisezione
Le formule di bisezione servono per calcolare il seno, coseno o tangente della metà di un angolo noto (bi - secare significa tagliare in due).
Dato che dimezzare e raddoppiare sono strettamente legati, essendo uno l'opposto dell'altro, partiamo dalle formule di duplicazone, in particolare quelle del coseno in quanto offrono degli elementi più maneggevoli:
Se è il doppio di , è la metà di . Chiamiamo quindi , e dividendo per due otteniamo che ; sostituendo otteniamo
A questo punto non ci resta che applicare la legge fondamentale per far rimanere una volta e l'altra solo . Iniziamo da quest'ultimo
Svolgendo i calcoli ed isolando otteniamo
In modo analogo elaborando la formula in modo che vi rimanga solo si ottiene
Purtroppo il significato di quel NON è che possiamo scegliere uno dei due segni, ma che NON SAPPIAMO quale sia quello giusto. Per questa ragione le formule di bisezione sono particolarmente SCOMODE, a meno che o non compaiano elevati al quadrato, nel qual caso si ha il doppio effetto di far sparire sia la radice che il doppio segno (che al quadrato diventerà comunque un ).
Nell'animazione di seguito spieghiamo, prima con un esempio numerico e poi con delle considerazioni più generali, come mai queste formule "non riescono a decidere" il segno del loro risultato.
Vediamo ora alcuni esempi di applicazione delle formule, verificando quando la questione del segno costituisce un problema e quando non lo è.
ESEMPIO 1: calcola il coseno di 15° e di 165°
15° è la metà di 30°, e sappiamo che il ; applichiamo quindi le formule di bisezione con questi angoli:
Dato che in questo caso SAPPIAMO che stiamo parlando di 15°, POSSIAMO DIRE che il suo coseno è positivo (è nel primo quadrante), quindi scegliamo il segno giusto
Vediamo ora come va con 165°
165° è la metà di 330°, che è 360° - 30° , quindi è un arco associato di 30°. Dalla figura vediamo che ha lo stesso coseno di 30°.
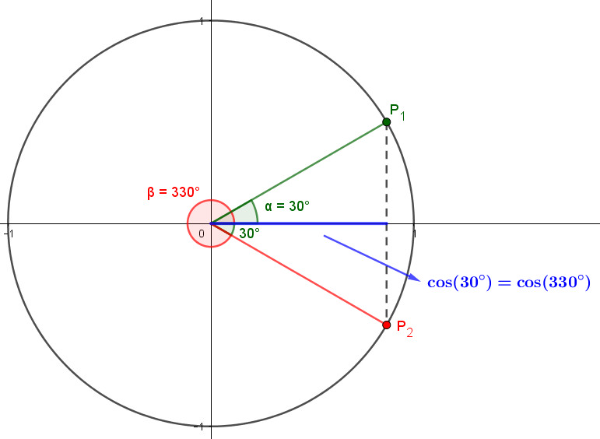
Abbiamo quindi che ; quando applichiamo di nuovo le formule di bisezione otterremo lo stesso risultato di prima:
Ovviamente abbiamo lo stesso risultato, incluso il doppio segno, e SOLO PERCHE' SAPPIAMO che stiamo parlando di 165°, POSSIAMO DIRE che il suo coseno è negativo (è nel secondo quadrante), e scegliere il segno giusto
ESEMPIO 2: un'equazione risolubile con le formule di bisezione
Consideriamo la seguente equazione
Notiamo che le due funzioni goniometriche hanno come argomento due angoli diversi; per prima cosa dobbiamo fare in modo che l'angolo incognito sia sempre lo stesso: o oppure . Poiché il compare elevato al quadrato, possiamo sostituire la relativa formula di bisezione, dato che spariranno sia il doppio segno che la radice.
A questo punto tutte le funzioni goniometriche presenti nell'equazione hanno come incognita l'angolo , e quindi possono essere combinate tra loro per risolvere l'equazione: svolgiamo i calcoli e risolviamo.
ESEMPIO 3: un'equazione che NON conviene risolvere con le formule di bisezione
Consideriamo la seguente equazione
L'equazione è molto simile alla precedente, ma questa volta NON è elevato al quadrato; ne consegue che se al suo posto sostituiamo la relativa formula di bisezione NON spariranno né il doppio segno né la radice, ed otterremo un'equazione molto scomoda da risolvere
Conviene allora lasciar stare e lavorare sul .
Se definiamo (e di conseguenza ) possiamo sostituire al posto di nell'equazione:
In altre parole al posto di dire che è la metà di , stiamo dicendo dire che è il doppio di , così possiamo usare ora le formule di DUPLICAZIONE, che sono più semplici di quelle di bisezione, per risolvere :
A questo punto in tutta l'equazione c'è sempre lo stesso angolo, ; ci resta solo da trasformare l'unico presente in tramite la prima legge fondamentale:
che svolgendo i conti diventa:
Abbiamo ottenuto un'equazione di secondo grado rispetto a . Dato che è scomparso il termine noto in questo caso possiamo scomporre raccogliendo ed applicare la legge di annullamento (altrimenti avremmo dovuto applicare la formula).
Il primo fattore è nullo quando , cioè (vai sul cerchio per verificarlo) quando .
DOBBIAMO RICORDARCI DI TROVARE , NON BASTA TROVARE . Recuperando la sostituzione che abbiamo fatto abbiamo
Da cui moltiplicando per abbiamo .
Allo stesso modo dobbiamo trovare i risultati per annullando il secondo fattore, e da questi ottenere i corrispondenti valori per .