Attività 1: posizione retta e circonferenza
Prepariamo il foglio di Geogebra
- Tracciamo una circonferenza sul piano: disegniamo un punto sul piano che sarà il nostro centro
e rinominiamolo con O (tasto destro sul punto: Rinomina]. Tracciamo una circonferenza di centro O e per un punto a piacere 
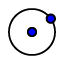; rinominiamo tale punto con C.
- Disegniamo due punti esterni alla circonferenza che rinomineremo con P e Q. Tracciamo la retta per P e Q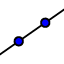
- Muoviamo
il punto Q in modo che la retta incontri la circonferenza in due punti. Individuiamo tali punti di intersezione con il comando intersezione 
. Rinominiamo tali punti con A e B. - Muoviamo il punto Q e osserviamo il comportamento dei punti A e B.
Riassumiamo le osservazioni svolte
Una retta è esterna quando
Una retta è tangente quando
Una retta è secante quando
Ancora sulla retta e la circonferenza
- Sempre utilizzando il foglio costruito sopra, misuriamo il raggio della nostra circonferenza. Utilizziamo il comando
distanza [che troviamo nel menù degli angoli]: scegliamo il punto O e il punto C. - Ora misuriamo la distanza della retta dal centro O della circonferenza. Utilizziamo lo stesso comando scegliendo il centro O e la retta r.
- Muoviamo
la retta spostando Q. Cosa possiamo osservare riguardo alla distanza della retta da O rispetto al raggio?
Teorema
Se la retta r è esterna alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è tangente alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è tangente alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è tangente alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Teorema
Se la retta r è secante alla circonferenza allora la distanza della retta dal centro O della circonferenza è
Il viceversa
- Costruiamo questo segmento con Geogebra:
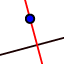b) individuiamo il punto di intersezione tra le due rette e 
rinominiamolo con H
c) tracciamo il segmento di estremi O e H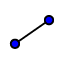 
e nascondiamo la retta perpendicolare disegnata al punto (a) [tasto destro sulla retta: mostra oggetto]
d) misuriamo OH
2. Scegliamo un punto sulla retta a piacere [punto su oggetto] 
(diverso da P, Q, H) e rinominiamolo con E.
3. Muoviamo la retta r (spostando Q o P) in modo che OH >r (OC); osserviamo:
OE è
perché:
Muovendo E sulla retta si osserva che OE è sempre maggiore di OH (eccetto per E=H) poiché
Poiché abbiamo scelto OH>r possiamo concludere che OE è
Possiamo concludere che
Se la distanza della retta r dal centro O della circonferenza (OH) è maggiore del raggio della circonferenza allora
- tutti i punti della retta avranno distanza da O maggiore del raggio
- non esistono punti in comune tra la retta e la circonferenza
- la retta è esterna alla circonferenza
Muoviamo adesso la retta in modo che OH=raggio
Ripetiamo quanto fatto sopra e proviamo a trarre le nostre conclusioni
Se la distanza della retta dal centro O (OH) è uguale al raggio della circonferenza allora:1) Tutti i punti della retta, eccetto H, hanno distanza dal centro O
poiché OE risulta essere
2) Il punto H della retta risulta avere distanza da O
3) Se OH= raggio allora la retta è
- ripetere quanto fatto sopra nel caso in cui OH<raggio cosa possiamo concludere?
Ricerca nel capitolo i risultati trovati e schematizza.
Svolgi l'esercizio proposto:
disegnare una circonferenza, scegli un punto sulla circonferenza e sfruttando il corollario disegna la retta tangente alla circonferenza e passante per il punto. [suggerimento: utilizzare retta perpendicolare]