Plateaukromme
De krommen worden genoemd naar de Belgische natuur- en wiskundige Joseph Plateau (1801-1883). Hij was gefascineerd door de waarneming van licht en ontwikkelde een draaiende schijf met een reeks tekeningen die door optische illusie de indruk van een bewegend beeld creëerde, de zgn. fenakistiscoop. Het is dus niet zonder reden dat de hoogste Belgische filmprijs naar hem genoemd wordt.
De vergelijking van de krommen is afhankelijk van niet minder dan drie parameters:
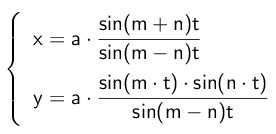
De factor a is enkel een schaalfactor en verandert de vorm niet. We onderzoeken daarom enkel de krommen voor a = 1.
Na de substitutie m/n = s houden we nog slechts één parameter over om de mogelijke vormen van de krommen te onderzoeken.
Start de animatie en volg de baan van het punt. Wanneer je de krommen toont, wordt snel duidelijk waarom we de meervoudsvorm gebruiken.
Verken volgende waarden van k:
- Wanneer k negatief is, bestaat de kromme uit een reeks hyperbolen. Voor k = -1 is er slechts één hyperbool.
- Wanneer k nadert naar 0, worden de hyperbolen rechten die naderen naar de x-as.
- Voor k = 0 is de kromme niet gedefinieerd.
- Wanneer k positief is, bestaat de kromme uit een reeks lussen en schuine asyptoten.
- Voor k = 0.25 is er één lus en één paar schuine asymptoten.
- Voor k = 0.5 is de vorm van de kromme een ellips.
- Ook voor k = 0.75 en k = 0.8 zijn er geen asymptoten.