Inyectiva, Sobreyectiva, Biyectiva e Inversa
1. Introducción
Supondremos que ya conocemos el concepto de una función (o aplicación) f entre dos conjuntos X (dominio) e Y (imagen):
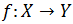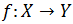Recordamos que si x es un elemento del dominio, X, su imagen mediante f es el elemento f(x) de Y. Por tanto, f(X) está contenido en Y.
Recíprocamente, si y es un elemento de Y, entonces puede existir un elemento x (pueden ser más de uno) tal que f(x) = y. Decimos que x es la anti-imagen de y.
En todo el texto trabajaremos con la función f con dominio X e imagen Y.
Recordamos que si x es un elemento del dominio, X, su imagen mediante f es el elemento f(x) de Y. Por tanto, f(X) está contenido en Y.
Recíprocamente, si y es un elemento de Y, entonces puede existir un elemento x (pueden ser más de uno) tal que f(x) = y. Decimos que x es la anti-imagen de y.
En todo el texto trabajaremos con la función f con dominio X e imagen Y. 2. Funciones Inyectivas
Una función es inyectiva si para todo x e y distintos de X sus imágenes f(x) y f(y) son distintas.
Es decir, una función es inyectiva cuando las imágenes de elementos distintos son distintas.
Ejemplos:
- La función identidad f(x) = x es inyectiva. La demostración es la siguiente: Supongamos que x e y son distintos. Entonces, f(x) es distinto de f(y) ya que f(x) = x que es distinto de y = f(y).
- La función nula f(x) = 0 no es inyectiva porque las imágenes siempre son 0. Por ejemplo, 1 es distinto de 2 pero sus imágenes son f(1) = 0 = f(2).
- La función no es inyectiva porque, por ejemplo. f(2) = 4 = f(-2).
3. Funciones Sobreyectivas
Una función es sobreyctiva (o suprayectiva) si todos los elementos de la imagen, Y tienen anti-imagen. Es decir, si para cualquier y de la imagen Y existe al menos un elemento x de la imagen tal que f(x) = y.
Notemos que esta propiedad es independiente de la inyectividad.
Ejemplos:
- La función identidad f(x) = x de los reales en los reales es sobreyectiva ya que cualquier real y tiene la anti-imagen x de X.
- La función f(x) = |x| de los reales en los reales no es sobreyectiva ya que los números negativos no tienen anti-imagen. La función f(x) = |x| considerada de los reales positivos en los reales positivos es sobreyectiva.
4. Función Biyectiva e Inversa
Una función es biyectiva si es inyectiva y sobreyectiva.
En tal caso, existe una función g, llamada función inversa, tal que para todo x del dominio,
y para todo y de la imagen
Normalmente, la función inversa de se denota por en lugar de .
Ejemplos:
- La función es biyectiva y su inversa es
- La función de los reales no negativos en los reales no negativos es biyectiva y su inversa es .