Matriz Inversa
Imagina que tienes la matriz cuadrada A y deseas obtener una matriz cuadrada B, que:
A*B = B*A = I (A multiplicado por B = matriz identidad)
Nota: Esta matriz B no siempre existe. Si existe esta matriz cuadrada B, se le llama matriz inversa de A y se denota como A-1.¿Cómo podemos hacer para encontrar B?
Te dejo un recurso para que revises el proceso de convertir una matriz A en su inversa (A-1), con el método de Gauss-Jordan.Matriz inversa: Método de Gauss
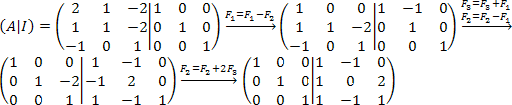
Ejercicio de aplicación
Propiedades
Matlab
Para encontrar la matriz inversa en Matlab u Octave, debes hacer lo siguiente:
Ingresa tu matriz de coeficientes (A):
A = [ 1 4 3; 2 5 4; 1 3 2 ]
Creamos la matriz identidad del tamaño de la matriz de coeficientes
I = eye( size( A ) )
Crea la matriz ampliada y la asignamos a la matriz B
B = rref( [A I ] )
Finalmente, extraemos la matriz inversa con la siguiente expresión:
B( : , 4:6)