El·lipse
L'el·lipse com a lloc geomètric.
Donats dos punts F1 i F2, que anomenarem focus, quin és el lloc geomètric dels punts del pla que la suma de les distàncies als focus sigui constant?
Tasca 1
En una finestra gràfica nova, dibuixeu dos punts i anomeneu-los F1(-3,0) i F2(3,0). A la línia d'entrada poseu: k=8. Inseriu un punt lliscant, anomeneu-lo d1 que prengui valors entre 0 i k amb increment 0.1. A la línia d'entrada poseu: d2=k-d1. Dibuixeu una circumferència de centre F1 i radi d1. Dibuixeu una circumferència de centre F2 i radi d2. Marqueu els dos punts d'intersecció de les dues circumferències. Activeu el traç d'aquest dos punts. Observeu que aquests dos punts compleixen que la suma de les distàncies als punts F1 i F2 és 8.
Moveu el punt lliscant d1 i veureu el lloc geomètric dels punts del pla que la suma de les distàncies als dos punts és 8. Es tracta d'una recta? Es tracta d'una circumferència? No, es tracta d'una corba anomenada el·lipse i els punts F1 i F2 s'anomenen focus de l'el·lipse.
GeoGebra té una eina per dibuixar el·lipses. Selecciona-la. Cliqueu sobre els punts F1 i F2 i sobre un punt negre del rastre. Observeu que l'el·lipse dibuixada coincideix amb el rastre negre. Observeu que a la Finestra algebraica ha aparegut un nou objecte i la seva expressió algebraica, és l'equació de l'el·lipse.
Tasca 2
L'equació general d'una el·lipse, centrada en l'origen amb focus F1(-c,0) i F2(c,0) i que la suma de les distàncies sigui k, és:
on a2 = k2/4 i b2 = a2 - c2
Tenint en compte aquesta fórmula i fent servir llapis i paper, trobeu l'equació de l'el·lipse centrada a l'origen de coordenades amb focus F1(-12,0) i F2(12,0) i que la suma de les distàncies sigui 26.
Introduïu la fórmula a la línia d'Entrada.
Ha sortit una el·lipse?
L'equació de l'el·lipse que es visualitza a la finestra algebraica és la mateixa que la que heu escrit? Has provat de clicar amb el botó dret sobre la fórmula?
Els valors d'a i de b de la fórmula de quina manera es visualitzen en el dibuix de l'el·lipse?
Utilitzeu el comandament Focus() per determinar els focus de l'el·lipse.
Tasca 3
Troba l'equació de les el·lipses següents:
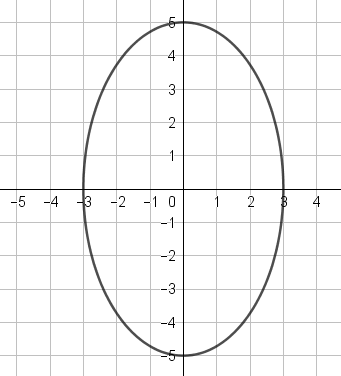
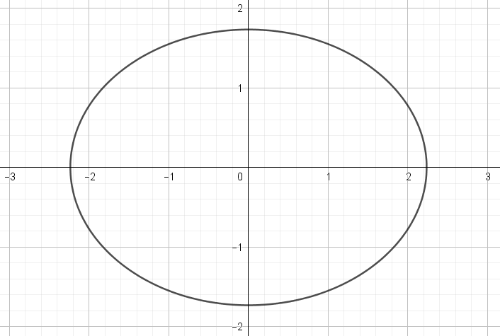
Tasca 4
Descarregueu la imatge següent al vostre ordinador (cliqueu amb el botó dret sobre la imatge i seleccioneu Anomena i desa). Amb l'eina Imatge, que trobareu al penúltim bloc d'eines, inseriu la imatge al GeoGebra. Amb l'eina Eli·lipse, intenteu ajustar l'arc del pont a una el·lipse.

Tasca 5
Amb la informació que us proporcionem a continuació, representa el Sol (un punt) i la Terra (un punt) dins la seva òrbita al voltant del Sol.
- L'orbita de la Terra al voltant del Sol té forma el·líptica.
- La distància màxima de la Terra al Sol es de 152,09 milions de km i la mínima és de 147,10 milions de km i s'assoleix al gener i al juliol.
- La distància entre la Terra en l'equinocci de primavera i la Terra en l'equinocci de tardo és de 299,148 milions de km.
Us esperàveu aquesta el·lipse?
Un cop situats el Sol i la Terra sobre la seva òrbita, cliqueu amb el botó dret sobre el punt que representa la Terra i selecciona Animació activada.
Accediu a les propietats d'aquest punt i a la pestanya Àlgebra canvieu la velocitat a 0.2. Què ha passat?
Tasca 6
Les el·lipses tenen una curiosa propietat que pots observar en aquesta construcció. Uns rajos de llum que sortissin del focus B en direcció a la corba, en rebotar, sortirien en direcció cap al focus A.
Feu la construcció anterior seguint els passos següents:
- Dibuixeu una el·lipse qualsevol amb l'eina El·lipse.
- Dibuixeu un punt D sobre l'el·lipse.
- Dibuixeu la recta tangent a l'el·lipse en el punt D.
- Dibuixeu la recta perpendicular a la recta anterior pel punt D.
- Feu una simetria de B respecte aquesta recta.
- Dibuixeu el segment BD.
- Dibuixeu la semirecta DA.