Übungen
Übung 1
Das Viereck $ABCD$ wird mit einer Kongruenzabbildung so bewegt, dass die Bildseite $[A'B']$ auf der Geraden $g$ zu liegen kommt ($A'$ angegeben). Vervollständige mit Längenabtragungen (Zirkel!) alle vier möglichen Bildvierecke.
Übung 2
Betrachte zwei zueinander kongruente Dreiecke $ABC$ und $DEF$. Wie viele Kongruenzabbildungen bilden $ABC$ auf $DEF$ ab, wenn die Dreiecke
- unregelmässig sind?
- gleichschenklig sind?
- gleichseitig sind?
Übung 3
Es gibt noch einen vierten bekannten Kongruenzsatz, genannt SsW. Recherchiere, was er besagt, und welche Bedingung dafür gelten muss. Warum ist diese Bedingung relevant? Was passiert, wenn sie nicht erfüllt ist?
Übung 4
Betrachte zwei beliebige, nicht unbedingt kongruente Vierecke $ABCD$ und $A'B'C'D'$. Ihre Seitenlängen seien mit $a=\overline{AB}$, $b=\overline{BC}$, usw. bezeichnet, ihre Winkel mit $\alpha=\angle DAB$ usw.
- Die Seitenlängen seien paarweise gleich lang: $a=a'$, $b=b'$, $c=c'$ und $d=d'$. Sind die Vierecke dann zwangsläufig kongruent? Begründe.
- Nenne eine weitere Bedingung, die zu denen in (a) hinzukommen muss, damit die Vierecke kongruent sind.
- In welchen weiteren Kombinationen von Seiten und Winkeln müssen die Vierecke übereinstimmen, um kongruent zu sein? Nenne mindestens zwei. Achte auf die gegenseitige Lage der Seiten und Winkel!
Übung 5
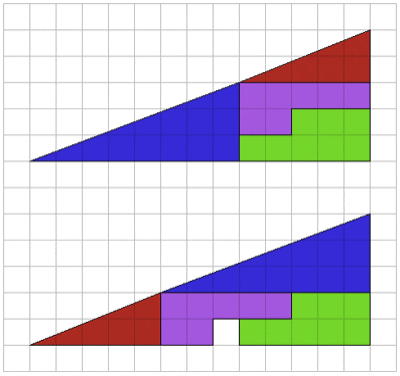
Die beiden Figuren sind in kongruente Teile zerlegt, haben aber offenbar nicht den gleichen Flächeninhalt! Was ist hier los?