Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

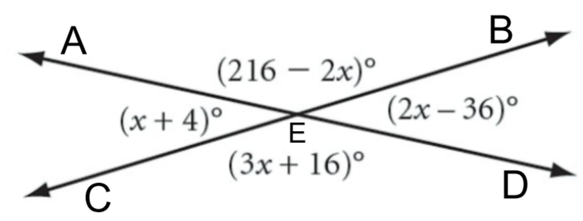
2.5 Angle Relationships

作者：knoche.danelle
When two lines intersect, they form four angles.  The point of intersection of the lines is the vertex of all four angles.  In the activity, you’ll investigate relationships between pairs of these angles.
Open the Geogebra box below and construct two intersecting lines.
Open the Geogebra box below and construct two intersecting lines.

Create 2 intersecting lines and label as shown above. Measure the 4 angles and display their measures on the screen.

What can you conclude about angles CEA and DEB? Drag points B and C around. Does the same relationship exist?

What kind of angles are angles CEA and DEB?

勾選所有適當的選項
  • A
  • B
  • C
核對我的答案 (3)

Fill in the blanks to complete a conjecture that is always true about vertical angles. Separate your answers with commas. If ______ angles are ___________ angles, then they are _____________. 

核對我的答案

What kind of angles are angles CEA and CEB?

勾選所有適當的選項
  • A
  • B
  • C
核對我的答案 (3)

What can you conclude about angles CEA and CEB? Drag points B and C around. Does the same relationship exist?

Fill in the blanks to complete a conjecture that is always true about linear pairs. If ____ angles form a ______________ of angles, then they ____________________________. 

Calculate the ratio of angles CEA and angles DEB.  The ratio is found by dividing the two angle measures.  What is the ratio of any vertical angles in your sketch? Will this ratio ever change, even if the angles change? Why? Does this convince you the vertical angle conjecture (above) is true?

Calculate the ratio of angle AEC and angle CEB.  The ratio is found by dividing the two angle measures.  What is the ratio of any linear pair in your sketch? Will this ratio ever change, even if the angles change? Why? Does this convince you the linear pair conjecture is true?

Image

Testing your understanding

x=

核對我的答案
Notes: Write your header for 2.5: Angle Relationships.  Write your 2 conjectures in your notes.  These are started in your book on page 132 and 133. They will be put on the board in a bit. Homework: On a sheet of notebook paper, complete p.134 #1-16 (you already did #12 above)

最新資源

探索資源

探索主題