Determinante de matrices
1. Introducción
La función determinante de una matriz es una herramienta que nos permite clasificar los sistemas de ecuaciones lineales según sus soluciones (Teorema de Rouché-Frobenius). La definición formal del determinante no es sencilla, pero existen reglas que facilitan su cálculo según la dimensión de la matriz. Sea una matriz de dimensión cualquiera, denotamos su determinante como ó como .
2. Determinante de dimensión 1x1
Sea una matriz de dimensión 1x1, es decir, la matriz es de la forma , entonces su determinante es
3. Determinante de dimensión 2x2
Sea una matriz de dimensión 2x2, es decir, una matriz de la forma

Entonces, su determinante es
Puede ayudar el siguiente diagrama:
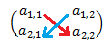
Por ejemplo
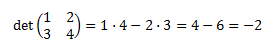
4. Determinante de dimensión 3x3
Sea una matriz de dimensión 3x3, es decir, de la forma

entonces su determinante es
![que es la llamada [b]Relga de Sarrus[/b]](https://stage.geogebra.org/resource/ZyGhe4ch/vgxzG1r10bQZNmp5/material-ZyGhe4ch.png)
![Ejemplo de la regla de Sarrus[b]
[/b]](https://stage.geogebra.org/resource/x7aXEa6Z/niPeUDp82cSdhg1B/material-x7aXEa6Z.png)
5. Determinante de dimensión mayor
Sea una matriz de dimensión , la representamos como , donde el elemento de la fila i y la comulna j (siendo ).
Llamamos a la matriz que resulta al eliminar la fila r y la columna s de .
Entonces, el desarrollo de Laplace del determinante de la matriz por la fila i es
![Laplace por la fila [i]i[/i][b]
[/b]](https://stage.geogebra.org/resource/jXh8B2z8/oCbdFZGcqKE1baY0/material-jXh8B2z8.png)
De forma similar, el determinante por la columna j de es
![Laplace por la columna [i]j[/i][b]
[/b]](https://stage.geogebra.org/resource/vdnrTUV4/VrB9QZyNUyHYuovp/material-vdnrTUV4.png)
Por ejemplo, para matrices de dimensión 3x3
![Laplace de la matriz de dimensión 3x3 por la fila 1[b]
[/b]](https://stage.geogebra.org/resource/xMmqdjsU/mutIr6SfAlrryci6/material-xMmqdjsU.png)
6. Más ejemplos
Aquí podemos encontrar más ejemplos del cálculo de determinantes de matrices.