This is not a circle
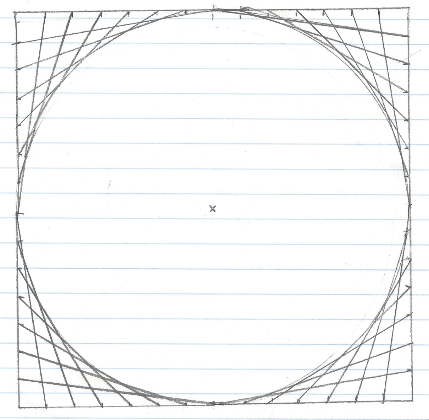
The envelope of the family of segments in this figure looks like a circle. But it is actually... something else!
By switching on the trace for the segment j you can make some lazy experiments how a quarter of the full circle-like curve looks like. Just move point E on the side AD.
Now type
Circle[C,B] to draw the conjectured circle. (You cannot directly select C or B in this figure by using the tools.) Clearly, there is a visible a gap between the circle and the red curve.Computing the envelope
By using the command
Envelope[j,E] you can find the exact curve.
Try zooming out or moving the curve to learn more about it. Do you have a conjecture which curve is this?Challenges
- Create the same figure from scratch in GeoGebra on your own.
- Check the equation of the envelope in the Algebra View. What order does it have? Does it confirm your conjecture?
- Find better positions for points A and B to get a curve with an equation which is easier to observe. You may want to show the grid and the axes.
- Try to create the envelope curve explicitly without using the Envelope command, but basic GeoGebra tools only.
- Now you will need to show that your curve is the same as the one that GeoGebra computed for you. This may be not straightforward because different equations will be shown (for the locus equation you will see an equation with integer coefficients, but for the other one the coefficients will be normed). A possible approach could be to create the intersection point P of the segment EE'' and your curve, then create a tangent line t to your curve at point P, finally lengthen the segment EE'' to a line. If the line EE'' and the tangent line are identical, then your curve must be correct! You may check out https://arxiv.org/abs/1704.08483, section 5.1 if you get stuck.