Monotonieverhalten und Extrempunkte
Die Bedeutung der ersten Ableitung f'(x)
Um das Folgende verstehen zu können, müssen Sie wissen (und am besten auch verstanden haben), was die Ableitung eigentlich bedeutet.
Merke: Die Ableitung f'(x) gibt die Steigung der Tangente des Graphen an der Stelle x an.
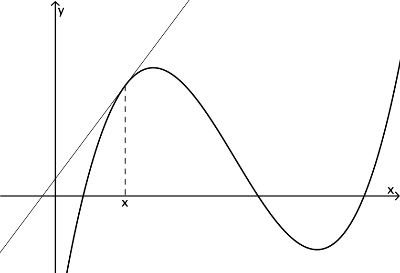
Die Steigung der Tangente an der Stelle x ist aber dieselbe wie die Steigung der Funktion f an dieser Stelle. Klicken Sie,um das zu sehen, im folgenden Applet den Punkt A an. Zoomen Sie nun diesen Bereich heran, indem Sie das Mausrad betätigen bzw. mit beiden Fingern über das Touch-Pad nach oben oder unten streichen.
Wir sehen also: An der Stelle x haben der Funktionsgraph und die Tangente dieselbe Steigung. Damit gibt die Ableitung nicht nur die Steigung der Tangente, sondern auch die Steigung des Graphen an der Stelle x an.
Merke: Die Ableitung f'(x) gibt die Steigung des Graphen an der Stelle x an.
Aufgabe
Ziehen Sie mit der Maus im folgenden Applet den Punkt A den Graphen einer Funktion f entlang. Beobachten Sie dabei die Werte der Tangentensteigung mt, d.h. der Ableitung f'(x).
Es gibt drei Stellen x, an denen die Steigung der Tangente mt null ist. Finden Sie diese.
Fazit
Als Ergebnis halten wir folgende Zusammenhänge fest:
- In Bereichen, in denen f'(x) < 0 (negativ) ist, da ist f streng monoton fallend.
- In Bereichen, in denen f'(x) > 0 (positiv) ist, da ist f streng monoton steigend.
- Hat f an der Stelle xH einen Hochpunkt, so ist dort die Tangente waagerecht, d.h. mt = f'(xH) = 0. Außerdem wechselt das Vorzeichen von mt, d.h. von f'(x) beim Übergang von links von xH nach rechts von + nach -.
- Hat f an der Stelle xT einen Tiefpunkt, so ist dort die Tangente waagerecht, d.h. mt = f'(xT) = 0. Außerdem wechselt das Vorzeichen von mt, d.h. von f'(x) beim Übergang von links von xT nach rechts von - nach +.
- Ein Terassenpunkt liegt vor, wenn gilt: mt = f'(xTP) = 0, und f'(x) hat rechts und links von xTP dasselbe Vorzeichen, wechselt also das Vorzeichen nicht.