Voorwaarden
Wij gaan nu na of het mogelijk is om met elke regelmatige veelhoek een regelmatig veelvlak te realiseren. Wij houden hierbij rekening met:
1° In elk hoekpunt van een regelmatig veelvlak
moeten evenveel zijvlakken samenkomen.
2° Alle hoeken van deze zijvlakken zijn even groot
omdat de zijvlakken regelmatige veelhoeken zijn.
3° Indien er in een hoekpunt van een veelvlak m zijvlakken samenkomen dan is de som van deze hoeken gelijk aan het aantal zijvlakken m, vermenigvuldigd met de grootte van deze hoek.
Aangezien in één hoekpunt van een regelmatig veelvlak minstens drie veelhoeken moeten samenkomen, maar de totale som van deze hoeken kleiner dan 360° moet zijn, is het aantal mogelijkheden bij de
keuze van de regelmatige veelhoek beperkt.
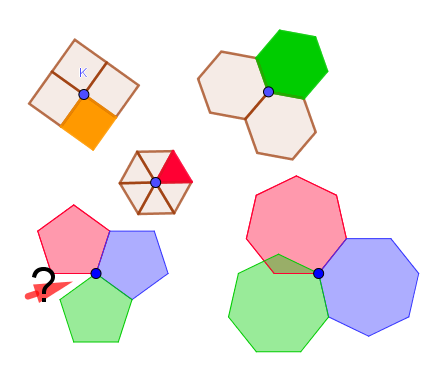
Eén van de mogelijkheden is het samenkomen van drie regelmatige vijfhoeken in één hoekpunt.
Zodoende kan je de verschillende mogelijke gevallen onderzoeken?
Met driehoeken kunnen verschillende regelmatige veelvlakken gevormd worden.
Twee vierkanten is te weinig.
Drie vierkanten is allicht mogelijk (denk aan een kubus).
Drie zeshoeken is niet mogelijk omdat deze alle drie in één vlak liggen.
Vier vijfhoeken is te veel omwille van de overlapping.