The Mid-segment of a Triangle
Essential Question: What is the mid-segment of a triangle and how is it useful in the real world?
Before we define the mid-segment of a triangle, let's look at a problem.
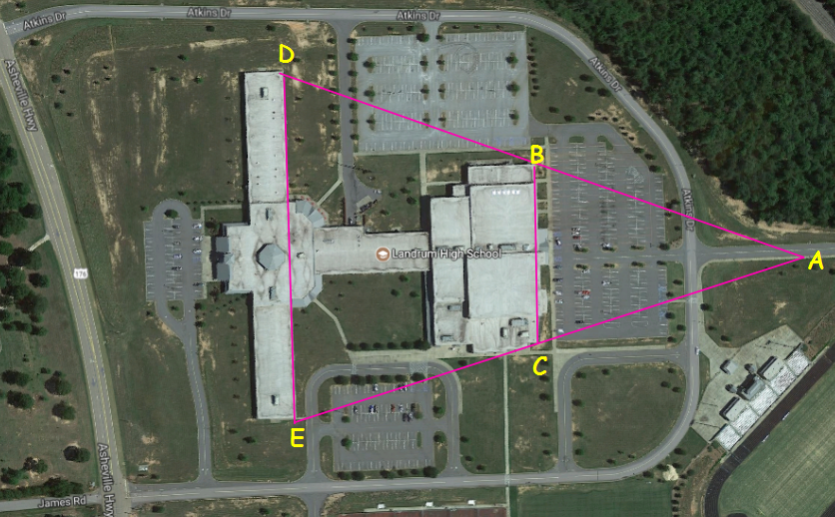
Below is an aerial photograph of Landrum High School in Landrum, SC. The problem discovered by maintenance is that the original plans contain the measurements of the front of the school DE (300 and 200 halls combined); however, the length of the back of the school BC is not been identified on the original plans. An isosceles triangle ADE has been layered on the map such that B and C are the midpoints of side DA and EA respectively. How can we find the length of the back of the school BC if the front of the school DE s approximately 770 feet?
Satellite View of Landrum High School
Discover the Mid-segment of a Triangle
Congratulations! You have just constructed the midsegment ED of triangle ABC. Now let's explore more facts about this line segment.
1. Compare the lengths of DE and BC. (Hint: Use the distance formula) What do you notice? SHOW YOUR WORK!
2. Calculate the slopes of DE and BC? What do you notice? Show work.
3. Look at your answers from questions #1 and #2. List two things you discovered about the mid-segment of a traingle.
The Midsegment of a Triangle Theorem
Now, let's solve the original problem.
Satellite View of Landrum High School
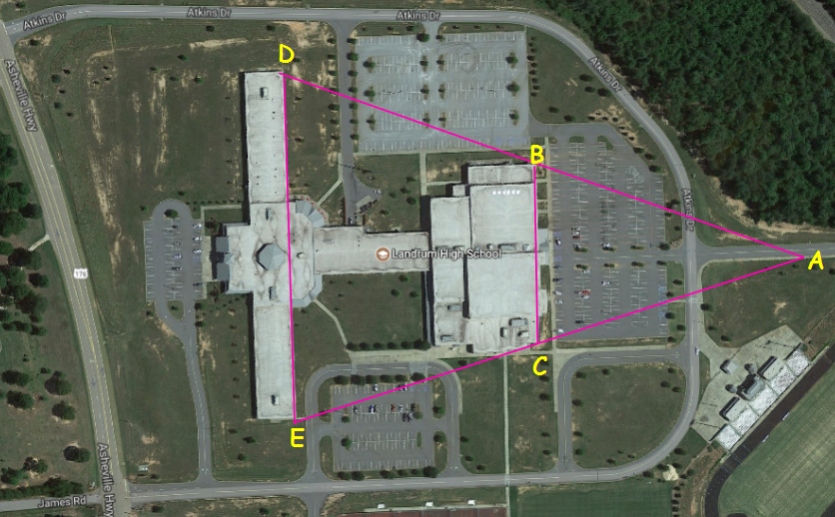
4. Since B is the midpoint of AD and C is the midpoint of AE, what do we know about segment BC in the photograph above?
5. Based upon your answers to questions #1-3 and the video above, what two things are true about segment BC?
6. What is the length of the back of the school BC if the front of the school is 770 feet?
Waclaw Sierpinski was a famous Polish mathematician that studied fractals. In mathematics, a fractal is an abstract object used to describe and simulate naturally occurring objects. If you create the three mid-segments of a triangle again and again, then what is created is the Sierpinski triangle. Watch the video below on how to create your own Sierpinski's triangle. After watching the video, take a handout and draw your own Sierpinski triangle. Use color and doodling to enhance your triangle. As a class, we will join our triangles to create on large triangle.