samengestelde intrest
Als je 1 jaar 100 euro uitzet tegen 3% ontvang je 100. 0,03 = 3 euro aan intresten.
Maar wat gebeurt er als deze intrest bij het kapitaal gevoegd wordt?
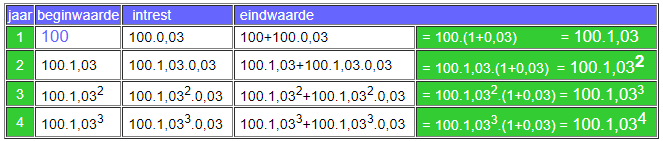
Tot welke eindwaarde zal het beginkapitaal van 100 euro zijn aangegroeid na 4 jaar?
rentefactor
- We noteren de rentevoeten voortaan decimaal:
i.p.v. p = 3% noteren we de rentevoet als i = 0,03
Dit betekent: 1 euro brengt op 1 jaar 0,03 euro op aan intresten.
- We zien in deze formule de factor 1,03 opduiken.
Dit is de rentefactor: u = 1 + i
eindwaarde
Een beginwaarde k, belegd tegen een rentevoet van i %, groeit na n periodes aan tot een eindwaarde K volgens de formule: K = k . u n
hierin is u de rentefactor = 1 + i (b.v.: met een rentevoet i =4% wordt u = 1 + 0,04 = 1,04)
Deze formule kan je omvormen om de verschillende grootheden te berekenen.