Konstrukcija uspravne trostrane prizme
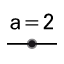 Pomoću alata Klizač definirajte stranice trokuta (a, b, c) i visinu pirmide h.
Pomoću alata Klizač definirajte stranice trokuta (a, b, c) i visinu pirmide h.
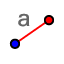 U Grafički prikaz pomoću alata Dužina zadane duljine nacrtajte dužinu duljine a (definirana je klizačem).
U Grafički prikaz pomoću alata Dužina zadane duljine nacrtajte dužinu duljine a (definirana je klizačem).
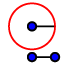 Pomoću alata Kružnica određena središtem i polumjerom, konstruirajte kružnicu sa središtem u točki A polumjera b (broj b je definiram klizačem), te kružnicu sa središtem u točki B polumjera c (također definiran klizačem).
Pomoću alata Kružnica određena središtem i polumjerom, konstruirajte kružnicu sa središtem u točki A polumjera b (broj b je definiram klizačem), te kružnicu sa središtem u točki B polumjera c (također definiran klizačem).
 Treći vrh trokuta je sjecište kružnica. Označite ga pomoću alata Sjecište.
Treći vrh trokuta je sjecište kružnica. Označite ga pomoću alata Sjecište.
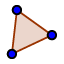 Spojite točke A, B, C pomoću alata Trokut, tako da završite u početnoj točki.
Spojite točke A, B, C pomoću alata Trokut, tako da završite u početnoj točki.
- Sakrijte sve nepotrebne linije (desni klik miša na objekt, opcija pokaži objekt)
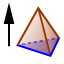 Nakon odabira alata Izvuci u piramidu kliknite na trokut u 3D grafičkom prikazu te upišite za visinu piramide broj h definiran klizačem.
Nakon odabira alata Izvuci u piramidu kliknite na trokut u 3D grafičkom prikazu te upišite za visinu piramide broj h definiran klizačem.
 Nakon što ste odabrali alat Pomicanje, mijenjajte veličinu piramide pomicanjem klizača, te pomičite piramidu miša uz pritisnutu lijevu tipku.
Nakon što ste odabrali alat Pomicanje, mijenjajte veličinu piramide pomicanjem klizača, te pomičite piramidu miša uz pritisnutu lijevu tipku.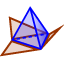 Nakon odabira alata Mreža, kliknite na piramidu. Otvorenost piramide kontrolirajte pomicanjem automatski izrađenim klizačem (u grafičkom prikazu).
Nakon odabira alata Mreža, kliknite na piramidu. Otvorenost piramide kontrolirajte pomicanjem automatski izrađenim klizačem (u grafičkom prikazu).
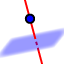 Pomoću alata Okomiti pravci konstruirajte visinu piramide klikom na njezin vrh i bazu.
Pomoću alata Okomiti pravci konstruirajte visinu piramide klikom na njezin vrh i bazu.
 Pomoću alata Sjecište označite nožište visine (sjecište pravca i baze).
Pomoću alata Sjecište označite nožište visine (sjecište pravca i baze).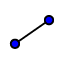 Alatom Dužina nacrtajte visinu tako da kliknete na točke vrha piramide i nožišta visine. Sakrijte pravac. Pomoću istog alata nacrtajte i dužinu od jednog vrha baze do nožišta visine.
Alatom Dužina nacrtajte visinu tako da kliknete na točke vrha piramide i nožišta visine. Sakrijte pravac. Pomoću istog alata nacrtajte i dužinu od jednog vrha baze do nožišta visine.
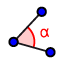 Izmjerite veličinu kuta što ga bočni brid zatvara s bazom odabirom alata Kut te odabirom tri točke (vrh piramide, vrh baze i nožište visine) ili odabirom bočnog brida i dužine koja spaja vrh i nožište visine.
Izmjerite veličinu kuta što ga bočni brid zatvara s bazom odabirom alata Kut te odabirom tri točke (vrh piramide, vrh baze i nožište visine) ili odabirom bočnog brida i dužine koja spaja vrh i nožište visine.
 Po potrebi možete izmjeriti veličinu bilo koje dužine (brida) odabirom alata Duljina te klikom na željenu dužinu.
Po potrebi možete izmjeriti veličinu bilo koje dužine (brida) odabirom alata Duljina te klikom na željenu dužinu.
 Nakon odabira alata Ravnina određena s tri točke kliknite na vrh piramide, jedan vrh baze (tamo gdje je već izmjeren kut) i nožište visine. U meniju koji se otvara desnim klikom miša na nacrtanu ravninu, odaberite opciju Prikaži u 2D prostoru u kojem će se pojavit presjek te ravnine i piramide.
Nakon odabira alata Ravnina određena s tri točke kliknite na vrh piramide, jedan vrh baze (tamo gdje je već izmjeren kut) i nožište visine. U meniju koji se otvara desnim klikom miša na nacrtanu ravninu, odaberite opciju Prikaži u 2D prostoru u kojem će se pojavit presjek te ravnine i piramide.
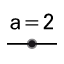 Pomoću alata Klizač definirajte stranice trokuta (a, b, c) i visinu pirmide h.
Pomoću alata Klizač definirajte stranice trokuta (a, b, c) i visinu pirmide h.
 U Grafički prikaz pomoću alata Dužina zadane duljine nacrtajte dužinu duljine a (definirana je klizačem).
U Grafički prikaz pomoću alata Dužina zadane duljine nacrtajte dužinu duljine a (definirana je klizačem).
 Pomoću alata Kružnica određena središtem i polumjerom, konstruirajte kružnicu sa središtem u točki A polumjera b (broj b je definiram klizačem), te kružnicu sa središtem u točki B polumjera c (također definiran klizačem).
Pomoću alata Kružnica određena središtem i polumjerom, konstruirajte kružnicu sa središtem u točki A polumjera b (broj b je definiram klizačem), te kružnicu sa središtem u točki B polumjera c (također definiran klizačem).
 Treći vrh trokuta je sjecište kružnica. Označite ga pomoću alata Sjecište.
Treći vrh trokuta je sjecište kružnica. Označite ga pomoću alata Sjecište.
 Spojite točke A, B, C pomoću alata Trokut, tako da završite u početnoj točki.
Spojite točke A, B, C pomoću alata Trokut, tako da završite u početnoj točki.
 Nakon odabira alata Izvuci u piramidu kliknite na trokut u 3D grafičkom prikazu te upišite za visinu piramide broj h definiran klizačem.
Nakon odabira alata Izvuci u piramidu kliknite na trokut u 3D grafičkom prikazu te upišite za visinu piramide broj h definiran klizačem.
 Nakon što ste odabrali alat Pomicanje, mijenjajte veličinu piramide pomicanjem klizača, te pomičite piramidu miša uz pritisnutu lijevu tipku.
Nakon što ste odabrali alat Pomicanje, mijenjajte veličinu piramide pomicanjem klizača, te pomičite piramidu miša uz pritisnutu lijevu tipku. Nakon odabira alata Mreža, kliknite na piramidu. Otvorenost piramide kontrolirajte pomicanjem automatski izrađenim klizačem (u grafičkom prikazu).
Nakon odabira alata Mreža, kliknite na piramidu. Otvorenost piramide kontrolirajte pomicanjem automatski izrađenim klizačem (u grafičkom prikazu).
 Pomoću alata Okomiti pravci konstruirajte visinu piramide klikom na njezin vrh i bazu.
Pomoću alata Okomiti pravci konstruirajte visinu piramide klikom na njezin vrh i bazu.
 Pomoću alata Sjecište označite nožište visine (sjecište pravca i baze).
Pomoću alata Sjecište označite nožište visine (sjecište pravca i baze). Alatom Dužina nacrtajte visinu tako da kliknete na točke vrha piramide i nožišta visine. Sakrijte pravac. Pomoću istog alata nacrtajte i dužinu od jednog vrha baze do nožišta visine.
Alatom Dužina nacrtajte visinu tako da kliknete na točke vrha piramide i nožišta visine. Sakrijte pravac. Pomoću istog alata nacrtajte i dužinu od jednog vrha baze do nožišta visine.
 Izmjerite veličinu kuta što ga bočni brid zatvara s bazom odabirom alata Kut te odabirom tri točke (vrh piramide, vrh baze i nožište visine) ili odabirom bočnog brida i dužine koja spaja vrh i nožište visine.
Izmjerite veličinu kuta što ga bočni brid zatvara s bazom odabirom alata Kut te odabirom tri točke (vrh piramide, vrh baze i nožište visine) ili odabirom bočnog brida i dužine koja spaja vrh i nožište visine.
 Po potrebi možete izmjeriti veličinu bilo koje dužine (brida) odabirom alata Duljina te klikom na željenu dužinu.
Po potrebi možete izmjeriti veličinu bilo koje dužine (brida) odabirom alata Duljina te klikom na željenu dužinu.
 Nakon odabira alata Ravnina određena s tri točke kliknite na vrh piramide, jedan vrh baze (tamo gdje je već izmjeren kut) i nožište visine. U meniju koji se otvara desnim klikom miša na nacrtanu ravninu, odaberite opciju Prikaži u 2D prostoru u kojem će se pojavit presjek te ravnine i piramide.
Nakon odabira alata Ravnina određena s tri točke kliknite na vrh piramide, jedan vrh baze (tamo gdje je već izmjeren kut) i nožište visine. U meniju koji se otvara desnim klikom miša na nacrtanu ravninu, odaberite opciju Prikaži u 2D prostoru u kojem će se pojavit presjek te ravnine i piramide.