abstract concepts and practice
portal of the Friday Mosque in Isfahan
On a portal of the Friday Mosque in Isfahan we can see this pattern. As
on the tympan and the spandrel of the arc on the Darb-e Imam a pattern of small
tiles is embedded into a pattern of bigger girih tiles.
Strictly spoken not self-similar
You can build up a Penrose tiling starting from one kite or dart by a repeated apply of the division rules on it, a process called inflation. Nowhere this proces is used by the Islamic decorators. They always start from a framework of bigger tiles filling it up with a second pattern different from the first one, even using patterns that don’t appear is the bigger framework. So, strictly spoken such patterns aren’t self-similar, they're just girih tiles of the same family. Lu and Steinhardt argue that it’s theoretically possible to keep on dividing leading to an aperiodic tiling.
Cromwell
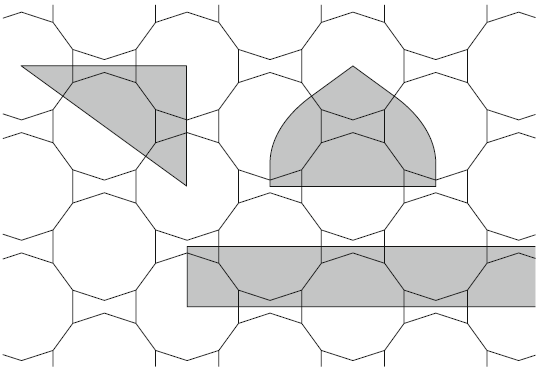
Cromwell doesn't feel comfortable with this reasoning. It looks as if the decorator, if only he would wanted to, would be able to cover an area with a pattern, starting with one tile, applying the division rules on it. But such a reasoning starts from western, modern abstractions. Sources prove that in Seljuk times a geometric knowledge on properties of pentagons and decagons was present. But categories as regular and irregular tilings weren’t used at that time. So it’s very tricky to apply them on the decoration practices. According to Cromwell, like the Topkapi scrolls, the patterns in Isfahan illustrate the intelligent practice to create multi-layered patterns. The first pattern isn’t randomly chosen. We can put the different patterns on the same background pattern of decagons and bow ties, one of the oldest and ubiquitous patterns, the crafstsmen were very familiar with. Upper left you can see the spandrel, upper right the tympan of the Darb-e Imam. Below there’s the strip of the portal of the Fryday Mosque of Isfahan.
Repeated division not workable in practice
Cromwell calculated the scale factor of the division rules to (rounded) 8,472. All forms become
more than eight times smaller with each division, what makes repeated division not-workable in practice. Two divisions of just one decagon would prduce 15 000 tiles. He concludes:
- It’s possible to produce quasi-periodic tilings starting from girih tiles using applying division rules or matching rules.
- Islamic artists used division to produce remarkable, very different hierarchic designs (see Topkapi scroll and Isfahan)
- There is no proof of iterated division. Only Two-layered patterns are known. The scale factor is very big and the area to cover is limited. For the patterns in de Topkapi scroll iteration is even impossible.
- The known patterns don’t proof that designers were aware of a process that could produce quasi-periodic patterns. Some are periodic, others multi-layered and not scale invariant.
Decorating a well-defined area
Cromwell notices too that (often at the corners) of the area to be decorates you can find deviations to the
dividing rules. Always it serves the aesthetic appreciation of the pattern, e.g. to fit a hexagon or decagon in a better way in a corner of a spandrel or tympan. The girih tiles and the skill to create a pattern within a given framework are very powerful tools to cover a well-defined area, whereas modern western mathematicians tend to call them ‘design errors’...
looking in detail...
An article of Peter Cromwell in Nexus Journal in 2016 is rather sobering for Lu & Steinhardt and all persons that tend to take all similarities with Penrose for reality. In a detailed analysis of a spandrel at the Friday Mosque in Isfahan Cromwell concludes that the workers acted rather pragmatic while realising two-layered designs. The aim was to fill a well-defined area in a satisfying way, not the general properties of a tiling. If this filling required different fillings, this was no problem. Even so if a wreath of circles resulted into overlapping decagons, 8-pointed stars were used instead of 10-pointed ones. The creative abilities of the
decorators is astonishing, but the picture of quasi-crystalline structures that Lu & Steinhardt held up doesn’t stand. Fortunately the creative richness stays, so keep on reading and exploring!

- Within a 10-pointed star of the 1st layer, we find a wreath of ... 8-pointed stars.
- The orange stars at the corners of the big 10-pointed star don’t fit quite well.
- The filling of the 5-pointed stars with forms of the 5-fold system matches well, but looking at the filling of the hexagons around them, the filling becomes very pragmatic with e.g. in the middle a very unusual form that doesn’t belong tot the 5-fold system.