Esquema
Elementi di analisi
Le caratteristiche principali che bisogna conoscere di una funzione per poterne stimare l'andamento sul piano cartesiano.
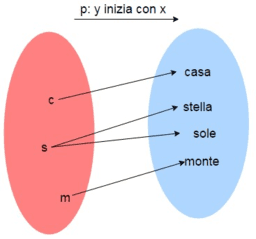
Tabla de contenidos
Caratteristiche generali delle funzioni
- Relazioni e funzioni: caratteristiche di base
- A cosa servono le funzioni?
- La funzione inversa
- Funzioni invertibili e non invertibili
- Funzioni pari e funzioni dispari; simmetrie
- Caratteristiche delle funzioni [1] - retta e parabola
- Caratteristiche delle funzioni [2] - esponenziali e logaritmi
- Caratteristiche delle funzioni [3] - goniometriche
- Esempi particolari di funzioni
- La risoluzione grafica di equazioni e disequazioni
Lo studio dei limiti
- Il concetto di limite - approssimazioni successive
- Visualizzatore di limiti - approssimazioni successive
- Limiti - un approccio più teorico
- La verifica formale dei limiti
- Verifiche formali di limiti e teoremi
- Visualizzatore di limiti - intorni
- Le funzioni continue
- Teoremi sulle funzioni continue
- Gli asintoti obliqui
Le derivate
- Visualizzare e studiare la velocità di un fenomeno
- La derivata come velocità istantanea
- Calcolare la derivata
- La funzione derivata
- Rapporto incrementale e derivata
- L'andamento della funzione e ricerca degli estremi
- Funzioni composte e loro derivate
- Derivate fondamentali e regole di derivazione
- Funzioni inverse e loro derivate
- I punti di non derivabilità
- Teoremi sulle funzioni derivabili
- Derivata seconda e concavità
- Esercizi sulla visualizzazione della derivata
- Problemi di ottimizzazione
- Applicazioni: meccanica
Gli integrali
- Gli integrali indefiniti
- Un esempio di funzione e sua primitiva
- Integrazione per sostituzione
- Visualizzazione delle primitive
- Gli integrali definiti: concetto e definizione
- La Funzione Integrale: definizione e proprietà
- Svelare il segreto dell'integrale definito: i teoremi
- Applicazioni: il valore medio di una funzione
- Costruire l'integrale giusto
- Applicazioni: il volume dei solidi di rotazione
- Piramide con base un triangolo isoscele (con animazione)