Ponto notável: Ortocentro
O ortocentro é a intersecção das alturas relativas aos três vértices, ou seja, é ponto de encontro entre todas as alturas de um triângulo.
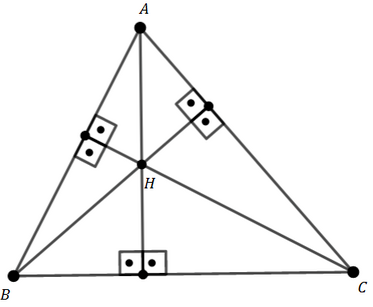
Observe a vídeo aula abaixo sobre como realizar a construção do ortocentro por meio da régua e compasso:
Caso ainda tenha dúvidas sobre como a reta suporte perpendicular foi gerada a partir de um ponto dado veja o material encontrado no link abaixo:
Observe o applet abaixo, onde possuímos um triângulo ABC qualquer e seu ortocentro... Movimente seus vértices e veja as alterações que ocorrem.
A partir do que foi observado no applet acima responda:
1) Se ABC for um triângulo acutângulo, o ortocentro fica localizado no:
2) Se ABC for um triângulo obtusângulo, o ortocentro fica localizado no:
3) Se ABC for um triângulo retângulo, o ortocentro fica localizado no:
Dados os conhecimentos acima, veja o problema abaixo:
"De um triângulo ABC, conhecemos as posições dos vértices B e C e do ortocentro D. Construa, com régua e compasso, o vértice A."
Resolução:
