Una "mica" més de complexitat
Reparametrització
Tenim dues corbes que volem fer servir per construir una superfície reglada però els valors límits dels seus respectius paràmetres no coincideixen. Què podem fer?
Suposem que el parametre de la primera corba varia entre a i b i el de la segona entre a' i b'. Podem trobar els valors de m i n de manera que:
a’ = m a + n
b’ = m b + n
Per a la primera corba farem servir el paràmetre t entre a i b i per a la segona m t + n també entre a i b. Això no sempre és factible.
És un sistema de dues equacions amb dues incògnites que té com a solució:
n=a' - m a
L'altra qüestió a tenir en compte és l'origen i el final de la superfície reglada. Hem de tenir molt clar a quins punts de la corba corresponen els valors a i a' d'una banda i b i b' d'una altra abans de començar a escriure comandaments. Veiem un exemple:- una corba amb paràmetre t de 0 a 1.
- una corba amb paràmetre s de -pi a pi.
No és trivial però no hi ha una altra manera si volem construir superfícies més complexes.
La volta de creueria
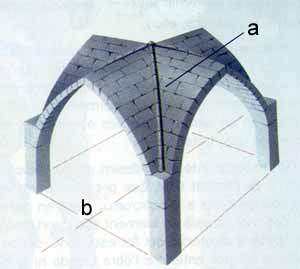
El procés pas a pas (els comandaments a la Línia d'Entrada en marró i negreta):
- Dibuixem la recta y=x.
- Dibuixem un punt A sobre la recta
. - Dibuixem el simètric A' d'aquest punt respecte de l'Eix Y
. - Dibuixem el quadrat que determinen A i A'
(cal posar 4 com número de vèrtexs). - Calculem la distància R de A al centre de coordenades: R=Distància(A,O).
- Construïm la circumferència de centre O i radi R: a=Corba(R cos(t), 0, R sin(t), t, 0, π / 2).
- La fem girar 45º respecte de l'Eix Z: a'=Rotació(a, π / 4, EixZ).
- També es pot fer servir l'eina
per a les rotacions. - Dibuixem la recta perpendicular al pla base pel punt D
. - Dibuixem un punt E sobre aquesta recta.
- Dibuixem el pla mitger del segment EB: PlaMitger(E, B).
- Trobem la intersecció G d'aquest pla amb la recta AB
i 
. - Calculem la distància del punt G al punt B: R'=Distància(G, B).
- Calculem l'angle α que formen els punts B, G i E
.
- Construïm l'arc de circumferència de centre G i radi R' c=Corba(x(G), y(G) + R' cos(t), z(G) + R' sin(t), t, 0, α).
d=Superfície(k c(t) + (1 - k) a'(m t), k, 0, 1, t, 0, α)
A partir d'aquí hem de construir les set superfícies que manquen per rotacions i simetries respecte dels plans x=0 i y=0 (recordeu que no ho podem fer amb les eines corresponents perquè no podem assenyalar superfícies):Rotació(d, π / 2, EixZ) Rotació(d, π, EixZ) Rotació(d, 3π / 2, EixZ)
Per les simetries amb els dos plans farem servir el comandament: Simetria(superfície,pla). A veure si us en sortiu!