Corollari
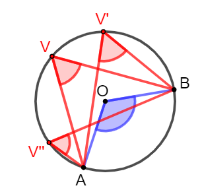
Corollario 1: angoli che insistono sullo stesso arco
Tutti gli angoli alla circonferenza che insistono sullo stesso arco, o su archi congruenti, sono congruenti.
Per dimostrarlo basta pensare che ogni angolo alla circonferenza è la metà dell'unico angolo al centro corrispondente. Quindi, tutti gli angoli alla circonferenza sono congruenti tra loro perchè sono tutti la metà dello stesso angolo.
Corollario 2: angoli che insistono su una semicircinferenza
Ogni angolo alla circonferenza che insiste su una semicirconferenza è retto.
Dimostrazione
Dato che l'angolo alla circonferenza è la metà dell'angolo al centro corrispondente, in questo caso deve essere la metà di un angolo piatto e quindi, si tratta di un angolo retto.
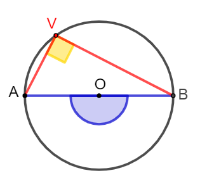
Inverso del corollario 2
Se un angolo alla circonferenza è retto, insiste su una semicirconferenza.
Dimostrazione
Se un angolo alla circonferenza è retto, l'angolo al centro corrispondente, dovendo essere il doppio, è piatto; quindi, i punti A, O, B sono allineati. E quindi, AB è un diametro e l'arco AB è una semicirconferenza.
Possiamo, quindi, dire che:
Un angolo alla circonferenza è retto se e solo se insiste su una semicirconferenza.
Tutti gli angoli che insistono su una semicirconferenza sono retti
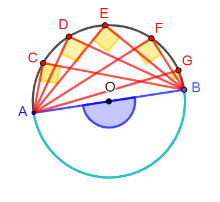
Osservazione
Tutti i triangoli inscritti in una circonferenza che hanno un lato che è un diametro della circonferenza sono rettangoli.
Triangoli inscritti in una semicirconferenza
Un triangolo inscritto in una semicirconferenza è un triangolo avente due estremi coincidenti con gli estremi della semicirconferenza e il terzo vertice in un punto qualsiasi della semicirconferenza.
Uno dei lati del triangolo, quindi, coincide con il diametro della circonferenza.
Si hanno delle proprietà interessanti:
- Un triangolo inscritto in una semicirconferenza è un triangolo rettangolo, la cui ipotenusa coincide con il diametro della semicirconferenza.
- La mediana relativa all'ipotenusa è uguale alla metà dell'ipotenusa. Infatti, la mediana è un raggio della circonferenza, mentre l'ipotenusa è un diametro.
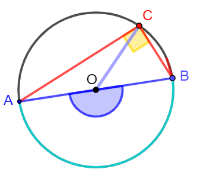
Mediana relativa all'ipotenusa
Dato che ogni triangolo rettangolo è sempre inscrivibile in una semicirconferenza il cui diametro è l’ipotenusa,
la mediana relativa all’ipotenusa è sempre la metà dell’ipotenusa stessa, per ogni triangolo rettangolo.