CAS Maxima via SageMath - fremdgehen CAS
Maxima/wxMaxima
ggb unterstützt keine lineare Programmierung (Simplex-Algorithmus) ich verwende das Opensource CAS Maxima/wxMaxima zur Bearbeitung/Überprüfung von Aufgabenstellungen.
wxmaxima-home-page
Alle Online-Dienste für das CAS Maxima wurden eingestellt. Als Ersatz ein Verweis auf SageMath!
ggb has no linear programm use opensource CAS Maxima/wxMaxima
Man kann das in SageMath integrierte Modul für Maxima verwenden oder auch direkt die leistungsfähigere aber komplexer aufgebauten Sage linear programming (LP) Module verwenden.
You can use the integrated Maxima module of SageMath or directly use the more powerful but more complex Sage linear programming (LP) modules.
Anwendungsbeispiel Linear Programm maximize/minimize
Application example Linear program maximize/minimize

CAS Maxima Instance of SageMath → LP Simplex
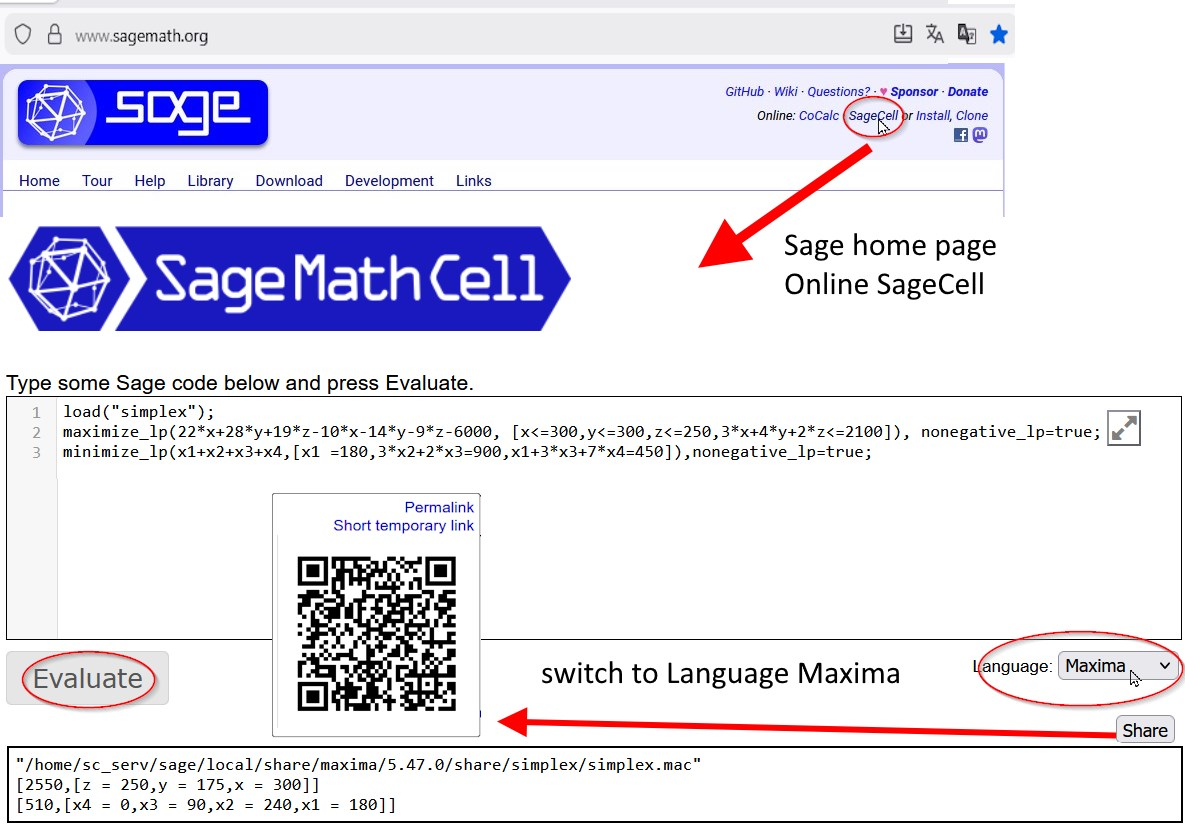
Maxima vs Sage
| minimize_lp(39*x1+21*x2+82*x3+55*x4, [ 2*x1+50*x2+6*x3+74*x4<=60, 2*x1+50*x2+6*x3+74*x4>=54, 1*x1+75*x2+13*x3+96*x4<=80, 1*x1+75*x2+13*x3+96*x4>=39, 5*x1+83*x2+5*x3+105*x4<=90, 5*x1+83*x2+5*x3+105*x4>=24, x1+x2+x3+x4=1 ]),nonegative_lp=true; [80/3,[x4=1/6,x3=0,x2=5/6,x1=0]] *.,numer; [26.66666666666668,[x4=0.16666666666667,x3=0,x2=0.83333333333333,x1= 0]] https://sagecell.sagemath.org/?q=zfwdbj https://maxima.sourceforge.io/docs/tutorial/de/maxima-einfuehrung.pdf https://www.albrecht57.de/images/stories/phgd/mathematik/computer/maxima_anleitung.pdf | p = MixedIntegerLinearProgram(maximization=False, solver='GLPK') v = p.new_variable(real=True, nonnegative=True) x1, x2, x3, x4 = v['x1'], v['x2'], v['x3'], v['x4'] p.set_objective(39*x1+21*x2+82*x3+55*x4) p.add_constraint(2*x1+50*x2+6*x3+74*x4<=60) p.add_constraint(2*x1+50*x2+6*x3+74*x4>=54) p.add_constraint(1*x1+75*x2+13*x3+96*x4<=80) p.add_constraint(1*x1+75*x2+13*x3+96*x4>=39) p.add_constraint(5*x1+83*x2+5*x3+105*x4<=90) p.add_constraint(5*x1+83*x2+5*x3+105*x4>=24) p.add_constraint(x1+x2+x3+x4==1) p.show() min=p.solve() print(p.get_values(x1,x2,x3,x4)) print('min=',round(min,3),'x1=',p.get_values(x1),'x2=',round(p.get_values(x2),3),'x3=',p.get_values(x3),'x4=',round(p.get_values(x4),3)) Minimization: 39.0 x_0 + 21.0 x_1 + 82.0 x_2 + 55.0 x_3 Constraints: 2.0 x_0 + 50.0 x_1 + 6.0 x_2 + 74.0 x_3 <= 60.0 -2.0 x_0 - 50.0 x_1 - 6.0 x_2 - 74.0 x_3 <= -54.0 x_0 + 75.0 x_1 + 13.0 x_2 + 96.0 x_3 <= 80.0 - x_0 - 75.0 x_1 - 13.0 x_2 - 96.0 x_3 <= -39.0 5.0 x_0 + 83.0 x_1 + 5.0 x_2 + 105.0 x_3 <= 90.0 -5.0 x_0 - 83.0 x_1 - 5.0 x_2 - 105.0 x_3 <= -24.0 1.0 <= x_0 + x_1 + x_2 + x_3 <= 1.0 Variables: x_0 is a continuous variable (min=0.0, max=+oo) x_1 is a continuous variable (min=0.0, max=+oo) x_2 is a continuous variable (min=0.0, max=+oo) x_3 is a continuous variable (min=0.0, max=+oo) [0.0, 0.8333333333333329, 0.0, 0.16666666666666707] min= 26.666 x1= 0.0 x2= 0.833 x3= 0.0 x4= 0.166 https://sagecell.sagemath.org/?q=sozgsh https://doc.sagemath.org/html/en/thematic_tutorials/linear_programming.html |
Übungsaufgaben/Exercise
| Ein Unternehmen fertigt drei Produkte P1,P2 und P3 auf einer Anlage, die in der Abrechnungsperiode insgesamt für 2.100 Zeiteinheiten [ZE] zur Verfügung steht. Die Fixkosten der Periode belaufen sich auf 6.000 GE. Produktionsprogramm für max Gewinn! P1........P2........P3 Produkte 22.......28......,..19 Stückerlöse 10.......14...........9 Variable Stückkosten ...3.........4...........2 Produktionszeit [Min/ME] 300.....300......250 Maximale Absatzmenge maximize_lp( 22*x+28*y+19*z-10*x-14*y-9*z-6000, [ x<=300, y<=300, z<=250, 3*x+4*y+2*z<=2100]),numer; [2550,[z=250,y=175,x=300]] Tablo:={ x3 = 250, x2 = 300, x1 = 300, 3 x1 + 4 x2 + 2 x3 = 2100, -12 x1 - 14 x2 - 10 x3 = -6000 } | Aus 5m langen und 3m breiten Platten sind drei Typen kleinerer Platten folgender Größe und Stückzahl zuzuschneiden: A: 4 x 2,5m -> 180 Stück, B: 3 x 1,5m -> 900 Stück, C: 2 x 1 m -> 450 Stück. Zuschneiden parallel zu den Plattenkanten. Minimiere die Anzahl der zerschnitten Platten. minimize_lp(x1+x2+x3+x4,[ x1=180, 3*x2+2*x3=900, x1+3*x3+7*x4=450]), nonegative_lp=true; [510,[x4=0,x3=90,x2=240,x1=180]] Tablo:={ x1 = 180, 3 x2 + 2 x3 = 900, x1 + 3 x3 + 7 x4 = 450, x1 + x2 + x3 + x4 = 0 } |
| |
Integer/Ganzzahl Simplex - Maxima vs SageMath
| maximize_lp( 1.5*x1+3.5*x2+3*x3+4*x4,[ 3*x1 + 1*x2 + 3*x3 + 4*x4 <= 315, 1*x1 + 2*x2 + 2.7*x3 + 4*x4 <= 270, 2*x1 + 5*x2 + 5.5*x3 + 3*x4 <= 400, x1 <= 30, x2 >= 12, x3 >= 20, x4 >= 10 ]), nonegative_lp=true, numer; [330.8571428571428,[ x4=35.71428571428572, x3=20.00000000000001, x2=36.57142857142857, x1=0]] | p = MixedIntegerLinearProgram(maximization=True, solver='GLPK') v = p.new_variable(integer=True, nonnegative=True) x1, x2, x3, x4 = v['x1'], v['x2'], v['x3'], v['x4'] p.set_objective(1.5*x1+3.5*x2+3*x3+4*x4) p.add_constraint(3*x1 + 1*x2 + 3*x3 + 4*x4 <= 315) p.add_constraint(1*x1 + 2*x2 + 2.7*x3 + 4*x4 <= 270) p.add_constraint(2*x1 + 5*x2 + 5.5*x3 + 3*x4 <= 400) p.add_constraint(x1 <= 30) p.add_constraint(x2 >= 12) p.add_constraint(x3 >= 20) p.add_constraint(x4 >= 10) p.show() min=p.solve() print(p.get_values(x1,x2,x3,x4)) print('min=',(min),'x1=',p.get_values(x1), 'x2=',(p.get_values(x2)),'x3=',p.get_values(x3), 'x4=',(p.get_values(x4))) |
| Branch & Bound set x4=35 | |
| maximize_lp( 1.5*x1+3.5*x2+3*x3+4*x4,[ 3*x1 + 1*x2 + 3*x3 + 4*x4 <= 315, 1*x1 + 2*x2 + 2.7*x3 + 4*x4 <= 270, 2*x1 + 5*x2 + 5.5*x3 + 3*x4 <= 400, x1 <= 30, x2 >= 12, x3 >= 20, x4 >= 10, x4=35 ]), nonegative_lp=true, numer; [330.5000000000001,[ x4=35, x3=20.0, x2=32.99999999999999, x1=10.00000000000004]] | Maximization: 1.5 x_0 + 3.5 x_1 + 3.0 x_2 + 4.0 x_3 Constraints: 3.0 x_0 + x_1 + 3.0 x_2 + 4.0 x_3 <= 315.0 x_0 + 2.0 x_1 + 2.7 x_2 + 4.0 x_3 <= 270.0 2.0 x_0 + 5.0 x_1 + 5.5 x_2 + 3.0 x_3 <= 400.0 x_0 <= 30.0 - x_1 <= -12.0 - x_2 <= -20.0 - x_3 <= -10.0 Variables: x_0 is an integer variable (min=0.0, max=+oo) x_1 is an integer variable (min=0.0, max=+oo) x_2 is an integer variable (min=0.0, max=+oo) x_3 is an integer variable (min=0.0, max=+oo) [10.0, 33.0, 20.0, 35.0] min= 330.5 x1= 10.0 x2= 33.0 x3= 20.0 x4= 35.0 |
| https://sagecell.sagemath.org/?q=epaxzr | https://sagecell.sagemath.org/?q=ypeaja |
