Looking through the Lens
What's behind the lens?

OBJECTIVE: To learn how to find the greatest common factor (GCF)
In previous lessons, you've learned about prime factorization, prime and composite numbers, factors and multiples, and divisibility rules.
Climbing Down Trees: https://www.geogebra.org/m/hxmuf2dg
Going Dutch: https://www.geogebra.org/m/xvdee7pg
Sifting Grains: https://www.geogebra.org/m/gamspcmt
In this lesson, we'll put these concepts together to find the GREATEST COMMON FACTOR (GCF), also known as GREATEST COMMON DIVISOR (GCD) or HIGHEST COMMON FACTOR (HCF).
The GREATEST COMMON FACTOR (GCF) of two or more counting numbers is the greatest counting number that evenly divides all the given numbers. If that number is 1, then the two numbers are said to be RELATIVELY PRIME. There are many approaches to finding the GREATEST COMMON FACTOR or GCF. The approach we'll use here will involve PRIME FACTORIZATION of the numbers whose GCF is being sought. The applet found in the lesson Climbing Down Trees can be used here. The prime factors obtained there can be listed for all the numbers and the common factors identified. The number obtained by multiplying the common factors is the GCF.
Example: What is the GCF of 16 and 24?
Prime factors of 16 : 2 x 2 x 2 x 2
Prime factors of 24 : 2 x 2 x 2 x 3
The product of the common factors, 2 x 2 x 2 (shown in red) is the GCF, which is 8.
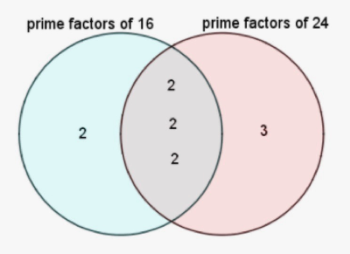
VENN DIAGRAM
A Venn Diagram can be used to visualize the concept of the GCF. Using the example above, we can list the common prime factors of 16 and 24 inside the lens (the intersection of the two sets). The other prime factors are listed inside their respective crescents. We now multiply the numbers inside the lens to find the GCF, which is 8.
A more compact method of finding the GCF is through CONTINUOUS DIVISION by prime factors, as illustrated below.
 Start by dividing by the smallest common prime factor, and repeat the process until no common prime factor can be found. Multiply the common prime factors at the left side to find the GCF.
The GCF is 2 x 2 x 2 or 8.
Here's an example using three numbers.
Start by dividing by the smallest common prime factor, and repeat the process until no common prime factor can be found. Multiply the common prime factors at the left side to find the GCF.
The GCF is 2 x 2 x 2 or 8.
Here's an example using three numbers.
 The GCF is 2 x 2 x 3 x 3 or 36.
The process just discussed is the systematic way of finding the GCF. For bigger numbers, an obviously common factor, NOT NECESSARILY PRIME, can be factored out first before the systematic process is applied. Consider this.
The GCF is 2 x 2 x 3 x 3 or 36.
The process just discussed is the systematic way of finding the GCF. For bigger numbers, an obviously common factor, NOT NECESSARILY PRIME, can be factored out first before the systematic process is applied. Consider this.
 The GCF is 10 x 2 x 3 x 7 or 420.
The GCF is 10 x 2 x 3 x 7 or 420.
Use the applet below for practice.
Enter 2 numbers in the entry boxes. Try solving the problem first on a separate sheet of paper, and then verify your answer by clicking Solutions. The GCF will appear below the numbers.
Click G.C.F. for 3 Numbers to work on 3 numbers, and follow the same procedure.
Repeat as many times as needed to master the concept.
In this lesson, you learned how to find the GREATEST COMMON FACTOR.
In the next lesson, you're going to learn how to find the LEAST COMMON MULTIPLE. Did you ENJOY today's lesson?