Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

Binomialverteilung

Autor:JulSza

Einführung

Zufallsexperimente, bei denen nur zwei Ausgänge (Treffer oder Niete, Erfolg oder Misserfolg) möglich sind, nennt man Bernoulli-Experimente. Führt man ein Bernoulli-Experiment mehrfach durch, so spricht man von einer Bernoulli-Kette. Heute geht es darum, die Formel herzuleiten, mit der man die Wahrscheinlichkeitsverteilung der Zufallsvariable X = "Anzahl der Treffer" bestimmen kann. Diese Verteilung nennen wir Binomialverteilung.

Kroos verwandelt in dieser Saison 15 von 20 Eltmetern.

Düsseldorf. Beim gestrigen Länderspiel der Nationalmannschaft gegen Frankreich verwandelte Toni Kroos seinen 15. Elfmeter in dieser Saison und führte die Mannschaft damit zum Sieg. Fünf Mal konnte der Spieler in dieser Saison vom Elfmeterpunkt das Runde nicht ins Eck bringen. Laut Statistikern beträgt die Wahrscheinlichkeit bei einen Elfmeter ein Tor zu erzielen bei 75%, was mit der Erfolgsquote des Spielers übereinstimmt. Die Fans sind gespannt, ob der Sportler in den nächsten Wochen weiter erfolgreich Elfmeter verwandeln wird. (Fiktiver Zeitungsartikel)
Toni Kroos am Elfmeterpunkt ([url=https://www.eurosport.de/fussball/elfmeter-kroos-bietet-sich-an_sto5677253/story.shtml]https://www.eurosport.de/fussball/elfmeter-kroos-bietet-sich-an_sto5677253/story.shtml[/url], letzter Zugriff: 17.09.2019)
Toni Kroos am Elfmeterpunkt (https://www.eurosport.de/fussball/elfmeter-kroos-bietet-sich-an_sto5677253/story.shtml, letzter Zugriff: 17.09.2019)

Aufgabe 1

Die Wahrscheinlichkeit, dass ein Spieler einen Elfmeter verwandelt, beträgt p=0.75. Bestimmen Sie die Wahrscheinlichkeit, dass der Spieler den Elfmeter verschießt. .

Revisa tu respuesta

Aufgabe 2

Berechnen Sie die Wahrscheinlichkeit mit Hilfe eines Baumdiagramms (siehe unten), dass Toni Kross bei den nächsten zwei Elfmetern keinmal, einmal oder zweimal trifft. Notieren Sie ihre Ergebnisse eine Tabelle. Zur Kontrolle: Trennen Sie ihre Ergebnisse bei der Eingabe durch ein "-", z.B. 0.25-0.33-0.75. Runden Sie auf zwei Nachkommastellen. Verwenden Sie die untenstehende Tabelle als Vorlage.

Revisa tu respuesta

Aufgabe 3

Berechnen Sie nun die Wahrscheinlichkeit mit Hilfe eines Baumdiagramms (siehe unten), dass Toni Kroos bei den nächsten drei Elfmetern keinmal, einmal, zweimal oder dreimal trifft. Notieren Sie ihre Ergebnisse eine Tabelle. Zur Kontrolle: Trennen Sie ihre Ergebnisse bei der Eingabe durch ein "-", z.B. 0.25-0.33-0.75. Runden Sie auf zwei Nachkommastellen. Verwenden Sie die untenstehende Tabelle als Vorlage.

Revisa tu respuesta
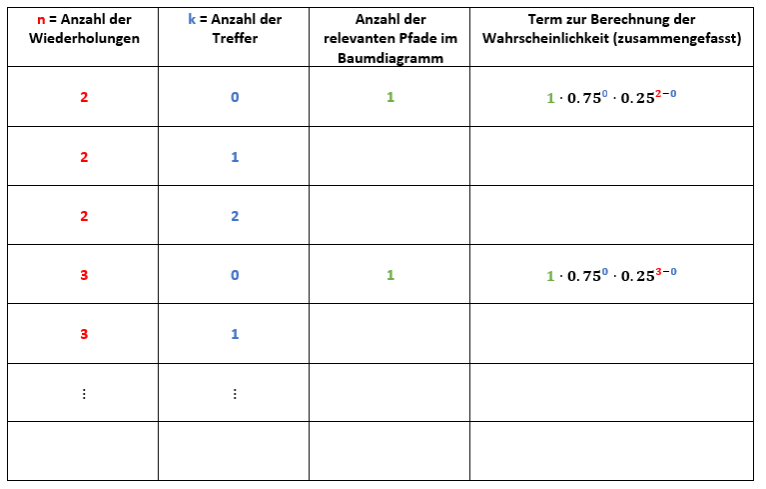
Image

Tempoaufgabe:

Betrachten Sie ihre Berechnungen in ihrer Tabelle. Können Sie Muster und Strukturen erkennen?

Aufgabe 4

Vergleichen Sie nun in ihrer Gruppe ihre Arbeitsergebnisse. Entwickeln Sie gemeinsam eine allgemeine Formel zur Berechnung der Wahrscheinlichkeit von k Treffern bei n Versuchen.

Aufgabe 5

Überprüfen Sie in Ihrer Gruppe ihre Formel, indem Sie drei Beispiele wählen und mittels des Taschenrechners berechnen. Überprüfen Sie ihre Lösung mit dem Geogebra-Applet. Um ihre Ergebnisse zu überprüfen, variieren Sie die Größen n, p sowie das k in .

Vertiefungsaufgabe

1) Bestimmen Sie mit Hilfe von Geogebra, wie groß die Wahrscheinlichkeit ist, dass Toni Kroos mindestens 17 Treffer bei 20 Elfmetern erzielt - gesucht ist also . 2) Bestimmen Sie mit Hilfe von Geogebra, wie groß die Wahrscheinlichkeit ist, dass Toni Kroos höchstens 17 Treffer bei 20 Elfmetern erzielt, gesucht ist also .

Nuevos recursos

Descubrir recursos

Descubre temas