Geometrische Bedeutung der Determinanten
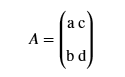
Zur Erinnerung: Die Determinante einer Matrix A ist die reele Zahl det(A)=ad-cb.
Man kann auch die Determinante zweier Vektoren berechnen, indem man diese als Spaltenvektoren einer Matrix auffasst.
Bsp.:
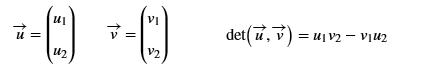
Gegeben seien nun die Vektoren
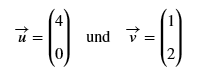
Berechne die Determinate der Vektoren. (Antwort in der Form det(u,v)=a*d-c*d=x)
Trage die Vektoren nacheinander in des Koordinatensystem ein (u startet im Ursprung und v am Endpunkt von u). Modelliere mittels -u und -v dann ein Parallelogramm.
Berechne nun den Flächeninhalt des Parallelogramms mithilfe der gewohnten Formel:
Tipp: Trage die Höhe in das Parallelogramm oben ein!
![(a=[AB] und h ist die Höhe des Parallelogramms)](https://stage.geogebra.org/resource/MDystYSy/ovzDcncbJvrvGdIS/material-MDystYSy.png)
Der Flächeninhalt des Parallelogramms beträgt
Vergleiche nun die Determinante mit dem Flächeninhalt des Parallelogramms.
Was fällt dir auf?
Hier kannst du deine Vermutungen noch einmal überprüfen.