Vendel koronája
Dr. Szilassi Lajos tanár úr egy régi évfolyamtársa, Kardos Lajos hívta fel a figyelmünket egy érdekes cikkre, ami 2014. 02. 26-án jelent meg a BME Haladvány Kiadványában, és amelynek szerzője Hujter Mihály. A cikk címe: Talpalattnyi arányosság.
Az írás szerzője egy 1936. márciusában megjelent KöMaL feladat kapcsán emlékezik meg egy kiváló szerzetes tanár, Endrédy Vendel (sz. Hadarits Kálmán) munkásságáról, annak neves tanítványairól. A cikket nyomatékosan ajánlhatjuk elolvasásra.
A probléma ami a cikkben megjelenik így fogalmazható meg:
Adjuk meg egy hegyesszögű háromszögben a talpponti háromszög és a hegyesszögű háromszög területének arányát a háromszög két szögének felhasználásával!
Hujter Mihály közöl egy megoldást, miszerint e keresett arány:
Ezt az arányt nevezte a szerző Vendel koronájának.
Dr. Szilassi Lajos tanár úr is adott egy megoldást, ezt mutatja a következő GeoGebra fájl.
Nem túl didaktikus módszer az, hogy egy egyszerűbb megoldás után egy bonyolultabbat mutatunk. Most mégis ezt tesszük, hogy miért, az talán az olvasó számára ki fog derülni.
A számolás végigkövethető ebben a GeoGebra CAS fájlban:
Látható, hogy a három bizonyítás három "különböző" trigonometrikus kifejezést adott eredményül. Ha mindegyik jó, akkor ezeknek egyenlőknek kell lenniük. Nézzük meg, hogy mit mond erről a GeoGebra CAS!
Úgy tűnik, hogy a három kapott kifejezés egyenlő. A pontos igazolás "lélekemelő" trigonometriai gondolatmeneteket igényel, ezeknek megalkotását az olvasóra bízzuk.
Ezek után felmerülhet az a kérdés, hogy a Vendel koronája arány hogyan változik az és szögek függvényében. Az ezt leíró kétváltozós függvény grafikonja az alábbi képen látható.
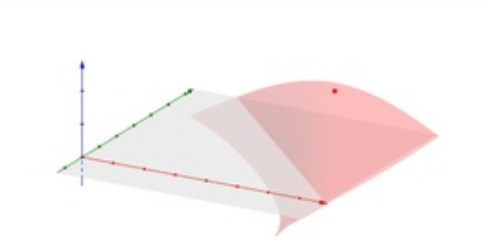
Ennek a kétváltozós függvénynek a szélsőértékét az alábbi GeoGebra CAS fájl adja meg.
Kaptuk, hogy a területarány szabályos háromszög esetében maximális, az értéke ez esetben .